
|

|

|
 |
 |

| Propósito de la sesión. Resolver
problemas sencillos de cálculo de
porcentajes en los que se deba determinar
e interpretar porcentajes menores al
100%. Construir tablas para usar técnicas
de proporcionalidad directa en la resolución
de cálculo de porcentajes.
Organización del grupo. Se sugiere trabajar en parejas durante toda la sesión. Materiales. Calculadora. |
| Eje |
| Manejo de la información. |
| Tema |
| Proporcionalidad. |
| Antecedentes |
| En la escuela primaria los alumnos resolvieron problemas de porcentaje en los que debían averiguar qué parte es una cantidad de otra; definieron el porcentaje de una cantidad como una fracción de la misma, y exploraron diversas estrategias para calcular porcentajes (por ejemplo, obtener porcentajes a partir del 10% y el 1% de una cantidad). En este grado de la escuela secundaria se continúa con la resolución de problemas de ese tipo haciendo el vínculo, en algunos casos, con el estudio de las ecuaciones de primer grado. |
| Propósitos de la secuencia
Resolver problemas que impliquen el cálculo de porcentajes utilizando de manera adecuada las expresiones fraccionarias o decimales. |
|||
| Sesión | Título y propósitos de la sesión | Recursos | Vínculos |
| 1 | México en el INEGI Resolver problemas sencillos de cálculo de porcentajes en los que se deba determinar e interpretar porcentajes menores al 100%. Construir tablas para usar técnicas de proporcionalidad directa en la resolución de cálculo de porcentajes. | Interactivo "Porcentajes" | |
| 2 | El IVA Resolver problemas de cálculo de porcentajes mayores al 100%. | Aula de medios "El IVA" (Hoja de cálculo) | |
| 3 | Miscelánea de porcentajes Resolver problemas que impliquen calcular y comparar porcentajes. | Video "Los migrantes" Interactivo "Porcentajes" | Español I secuencia 10 ¿La jaula de oro? |

Sugerencia didactica. La resolucion
de este problema implica aplicar un
porcentaje a una cantidad para obtener
otra cantidad; en este caso, se trata de
aplicar el 13% a 110 000 000. Se espera
que los alumnos tengan ya una noción
de porcentaje y que cuenten al menos
con un procedimiento para calcularlo;
sin embargo, es probable que algunos no
lo recuerden. Por ello, pídales que lean
la información que se les presenta en el
recuadro, aclare que 13% quiere decir
"13 de cada 100", y que en este caso
se trata de calcular 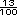 de 2 000 000. de 2 000 000.
Posibles procedimientos. Una forma de resolver es aplicar sucesivamente las dos operaciones: primero dividir 2 000 000 entre 100, y después multiplicar ese resultado por 13. Otra forma es mediante el algoritmo de la multiplicación por una fracción que estudiaron en la secuencia 10. Respuesta. 260 000 km2. |

Respuestas.
|

Sugerencia didáctica. Es posible
que algunos alumnos se percaten de
que la respuesta que dio el equipo
es equivocada, pero que no puedan
identificar por cuál nuúero se debió
haber multiplicado. Una vez que hayan
expresado sus respuestas enfatice que
calcular 13% de 2 000 000 implica
multiplicar 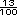 por 2 000 000, y que
esa fracción también puede expresarse
como 0.13; por lo tanto, los alumnos
de la otra escuela debieron haber
multiplicado por 0.13 por 2 000 000, y que
esa fracción también puede expresarse
como 0.13; por lo tanto, los alumnos
de la otra escuela debieron haber
multiplicado por 0.13 |
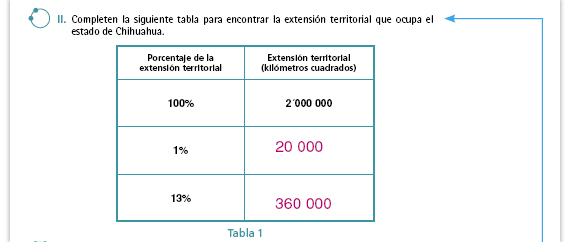
| Propósito de la actividad Utilizar tablas para que los alumnos identifiquen y se apoyen en algunas propiedades de la proporcionalidad que les permitan resolver este tipo de problemas. |

Respuestas.
Sugerencia didáctica. Reproduzca la tabla en el pizarrón y enfatice lo siguiente:
|
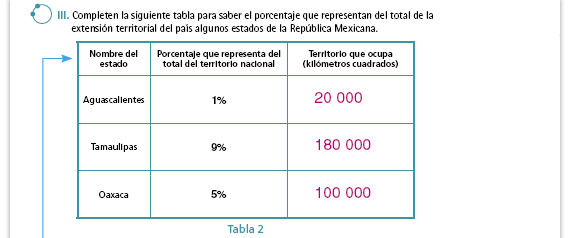
| Sugerencia didáctica. Lea junto con los alumnos la información de la tabla y pregúnteles en qué consiste la actividad. Recuérdeles que la cantidad que representa el 100% del territorio nacional es 2 000 000 km2. De acuerdo con lo que hicieron en la actividad anterior, pregunte al grupo: ¿Por cuánto deben multiplicar en cada uno de los casos para obtener el territorio que ocupa cada estado? Si nota que los alumnos aún tienen dificultades para resolver esta actividad, pueden completar la tabla en grupo. También puede hacerles notar que a partir de la obtención del 1% del territorio nacional (Aguascalientes), puede calcularse lo que corresponde al resto de los estados. |

 A partir del ejemplo que aquí se da,
destaque lo siguiente:
A partir del ejemplo que aquí se da,
destaque lo siguiente:
|
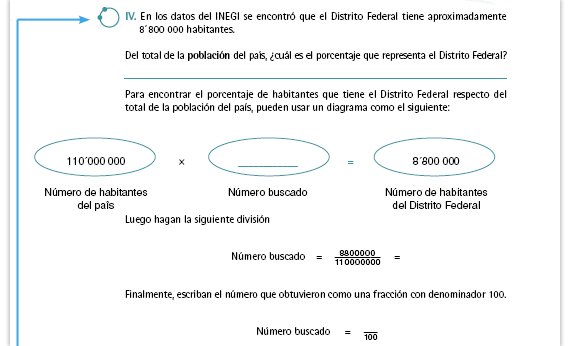
| Propósito de la actividad. Se trata de
determinar el porcentaje que representa
una cantidad con respecto a otra. Los
alumnos deberán averiguar qué porcentaje
representan 8 800 000 habitantes si el
100% son 110 000 000 habitantes.
Sugerencia didáctica. Antes de que los alumnos resuelvan, pídales que hagan una estimación: ¿Será el 50%? ¿Será más o menos del 50%? Posibles procedimientos. Es probable que los alumnos no conozcan una forma sistemática de resolver este tipo de problemas, por lo que pueden hacer una estimación y luego irse aproximando al resultado poco a poco. Por ejemplo, si suponen que es alrededor del 10% y hacen el cálculo aplicando ese porcentaje, obtendrán la cantidad de 11 millones, que es cercana a 8 800 000. A partir de ahí pueden probar con otros porcentajes menores hasta llegar al 8%, que es el porcentaje correcto. No es necesario que espere a que todo el grupo termine ni que lo resuelvan correctamente, pues la misma lección ofrece de inmediato un procedimiento de resolución; lo importante es que los alumnos tengan la oportunidad de enfrentarse al problema. |

| Sugerencia didáctica. Aproveche este momento de comparación de respuestas, para hacer algunas precisiones sobre el procedimiento que se sugiere. Reproduzca en el pizarrón el diagrama de la lección y plantee a los alumnos las siguientes preguntas: ¿Cuál es la operación que nos permite encontrar el número buscado? ¿Cuál es la operación inversa de la multiplicación? Una vez que los alumnos hayan identificado esa operación (lo estudiaron en la secuencia 18), señale que en este tipo de problemas, en los que se trata de determinar qué porcentaje representa una cantidad, el número buscado es una fracción con denominador 100 o un número decimal. |
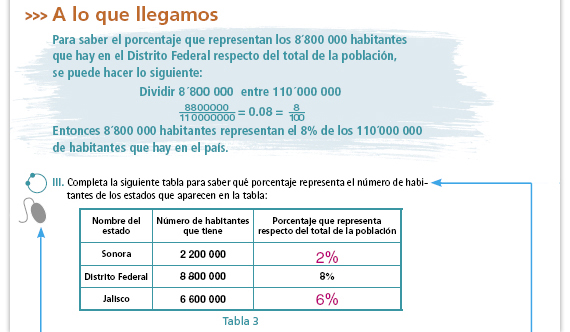
| Propósito del interactivo. Resolver problemas que impliquen el cálculo de porcentajes. | Integrar al portafolios. Si identifica que los alumnos tienen dificultades para resolver este problema, revise nuevamente con ellos el procedimiento que se describe en el último apartado A lo que llegamos de esta sesión. Además, cuando se haga la revisión colectiva de los resultados, usted puede plantear preguntas como las siguientes: ¿Qué número multiplicado por 110 000 000 da 2 200 000? ¿Qué número multiplicado por 110 000 000 da 6 600 000? Los alumnos deben concluir que ese número es el porcentaje que encontraron pero expresado con una fracción o con un número decimal. |