Propósito de la sesión. Resolver problemas de cálculo de porcentajes mayores al 100%. Organización de grupo. Se sugiere que los alumnos trabajen en parejas durante toda la sesión.

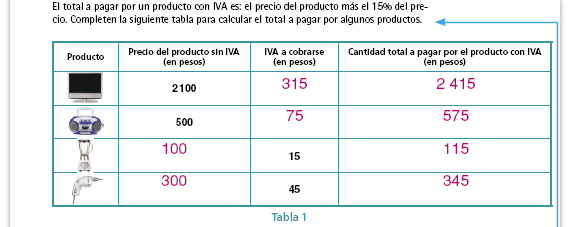
Sugerencia didáctica. En los dos primeros renglones se trata de aplicar un porcentaje a una cantidad para obtener otra cantidad. Puede recomendar a los alumnos que revisen nuevamente el primer apartado A lo que llegamos de la sesión anterior (deben multiplicar el precio del producto sin IVA por o por 0.15). En los dos renglones siguientes se trata de que a partir de una cantidad que representa un porcentaje (el 15%), se calcule la cantidad que representa el 100%. Es probable que los alumnos tengan mayores dificultades para este último tipo de problemas. Permita que intenten resolverlos aun cuando no logren completar toda la tabla.

Sugerencia didáctica. Reproduzca la tabla en el pizarrón para hacer el siguiente análisis con los alumnos: -En la primera columna, para pasar del 15% al 1%, dividimos entre 15; por lo tanto, en la segunda columna también debemos dividir $45 entre 15. Obtenemos $3. -Para pasar del 1% al 100% en la primera columna, multiplicamos por 100. De la misma manera, en la segunda columna multiplicamos $3 por 100, y obtenemos $300, que es el precio del taladro sin IVA.

Propósito de la pregunta. Que los alumnos se familiaricen con el hecho de que una cantidad representa el 100% de sí misma, esto les permitirá darle sentido a los porcentajes mayores de 100.

Sugerencia didáctica. Una vez que los alumnos hayan comparado y corregido sus respuestas, haga un análisis similar al que se sugiere para el caso del taladro: Porcentaje Cantidad correspondiente al porcentaje 15% $15 1% $1 100% $100 -Para pasar del 15% a 1% en la primera columna, se divide entre 15; de la misma manera, en la segunda columna se divide $15 entre 15, y se obtiene $1. -Para pasar de 1% a 100%, se multiplica por 100 en la primera columna. Por lo tanto, en la segunda columna también se multiplica $1 por 100. -Enfatice que el 100% de una cantidad puede interpretarse como 100 partes de 100.

Antes de que las parejas resuelvan el problema inicial, invite a los alumnos a leer el recibo que se les presenta. Pueden comentar a qué se refieren algunos de los conceptos que aparecen en el recibo, como renta, larga distancia internacional, etcétera. Esto les permitirá tener una idea más clara sobre el contexto del problema que se está trabajando, lo que a su vez les ayudará a tener un mayor control sobre sus procedimientos y resultados.

Posibles procedimientos. Es muy probable que los alumnos tengan dificultades al resolver este problema, pues es la primera vez que enfrentan una situación en la que el total representa más de un 100%. Una forma de determinar el subtotal del mes es por ensayo y error: estimar una cantidad, obtener el 15% de ella, sumar la cantidad con su 15% y ver si se obtiene 2 300. Si no es así, pueden ir aumentando o disminuyendo la cantidad que estimaron inicialmente hasta dar con la correcta. Un posible error es que calculen el 15% de 2 300, que es el total a pagar. Permita que exploren el problema y que lo resuelvan con los procedimientos que ellos decidan; posteriormente, en la sección Manos a la obra podrán conocer formas correctas de resolver el problema. Respuesta. a) $300. b) $2 000 (restando el subtotal a 2 300 se encuentra el IVA).

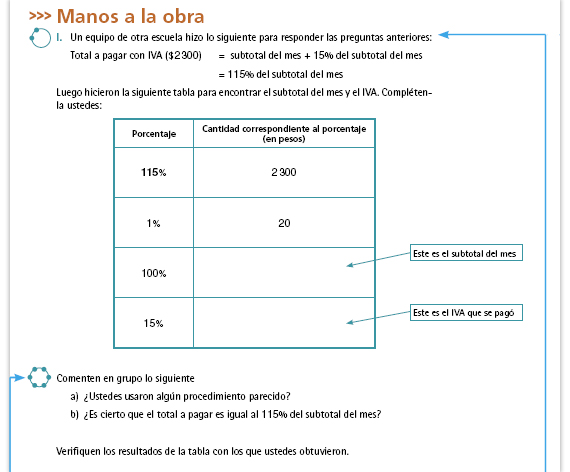
Sugerencia didáctica. Reproduzca la tabla en el pizarrón para que alguna pareja pueda registrar en ella sus respuestas; pida a esa pareja que explique cómo encontraron los resultados. Una vez que todo el grupo esté de acuerdo con las respuestas, comenten los incisos a) y b). Es importante que a los alumnos les quede claro que efectivamente el total a pagar es igual al 115% del subtotal del mes, porque ese porcentaje resulta de sumar el 100% del precio con el 15% del IVA.

Propósito de la actividad. Que los alumnos conozcan un procedimiento de solución que se basa en la elaboración de tablas y en algunas propiedades de la proporcionalidad.

Sugerencia didáctica. Invite a los alumnos a resolver el problema utilizando la tabla de la manera en que se mostró en el problema anterior.

Respuestas. a) $500. Se divide 575 entre 115 para obtener el 1%, luego se multiplica por 100. b) $250.

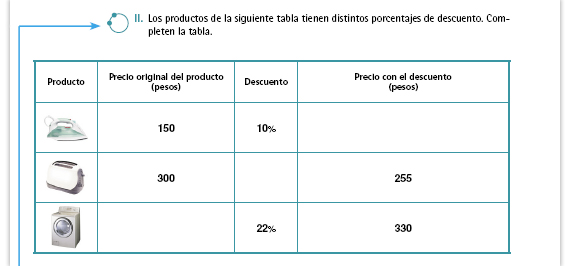
Integrar al portafolios. Si advierte que los alumnos tienen dificultades para completar la tabla, analice junto con ellos cada uno de los casos para que identifiquen cuál es el dato que se desconoce y qué es lo que tienen que hacer: aplicar un porcentaje a una cantidad (primer renglón de la tabla), determinar qué porcentaje representa una cantidad con respecto a otra (segundo renglón) y determinar la base de un porcentaje (tercer renglón). Según sea la manera en que se utiliza el porcentaje en cada caso, revise con ellos nuevamente el apartado A lo que llegamos de esta sesión y de la sesión 1. Sugiérales también que elaboren tablas para resolver aquellos casos que les resulten más difíciles. Respuestas. -Para el caso de la plancha, el 10% de 150 son $15. Se resta 150 - 15, el precio es $135. -Para el tostador, la diferencia entre el precio original y el precio con descuento es de $45, y 45 es el 15% de 300. -Para la lavadora, el precio original es de $423.07. El precio con el descuento es el 78% del precio original.