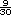Propósito de la sesión. Elaborar e interpretar tablas de frecuencia relativa. Organización del grupo. Forme parejas de alumnos para las dos primeras partes de la sesión y equipos para la tercera. La última se sugiere que la resuelvan de manera individual.

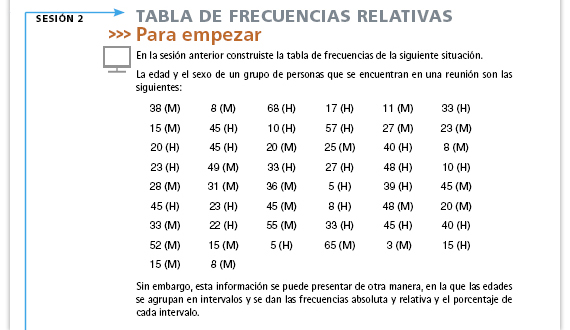
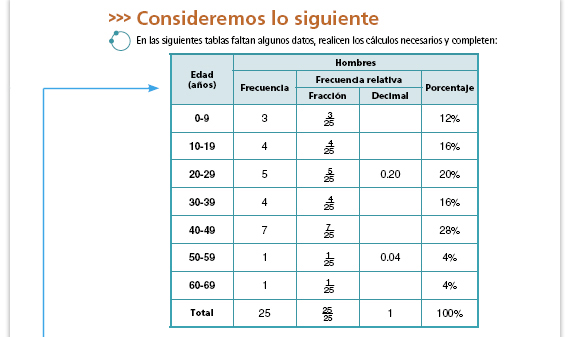
Sugerencia didáctica. Comente con los alumnos la información de las tablas. Los datos están organizados por género y por intervalos de edad: se cuenta a todas los hombres (o mujeres) que tienen de 0 a 9 años y el resultado se pone en la columna de frecuencia. Se va haciendo lo mismo con las que tienen de 10 a 19, de 20 a 29, etcétera. La columna de "frecuencia relativa" está dividida en dos para expresarla con una fracción y con un número decimal. La fracción puede leerse así: "3 de cada 25 hombres tienen entre 0 y 9 años". Diga a los alumnos que pueden utilizar la calculadora para encontrar la expresión decimal de la frecuencia relativa. La columna de "porcentaje" puede interpretarse como: "del total de hombres, el 12% tienen entre 0 y 9 años". Puede preguntar a los alumnos: si el total de hombres fuera 100 y el 12% tuvieran entre 0 y 9 años ¿cuál sería la frecuencia?, ¿cuál sería la frecuencia relativa?

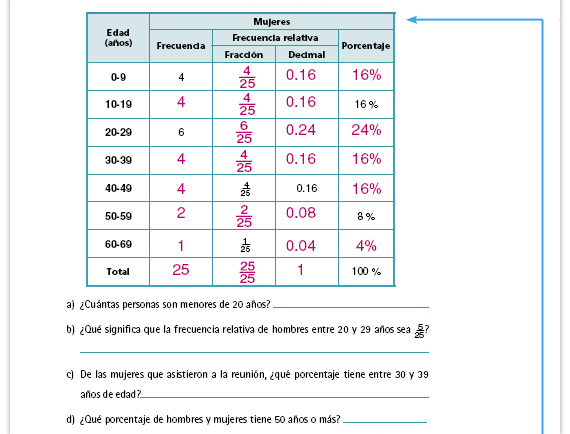
Sugerencia didáctica. Es conveniente hacer notar a los alumnos la relación entre la columna de "Frecuencia relativa" y la de "Porcentaje". Puede hacerles preguntas como: ¿De qué manera obtuvieron los datos de la columna "Porcentaje"?, ¿en qué se parecen a los de la columna "Frecuencia relativa"? Integrar al portafolios. Cuando terminen de resolver la sesión 2 pida a los alumnos una copia de esta tabla llena y de las respuestas a las preguntas de los incisos a) al d). Analícelas para ver si han comprendido la diferencia entre la frecuencia absoluta y la relativa, y sobre su expresión como porcentaje. Si lo considera necesario, repasen la sesión.

Propósito de la actividad. Con las preguntas planteadas en los incisos a) al j) se pretende que los alumnos le den sentido a la frecuencia relativa (su significado y obtención), así como a las diferentes formas en que se puede expresar (como porcentaje, fracción o decimal). Respuestas. a) 7 intervalos. b) 25 hombres y 25 mujeres. c) Hay 7 hombres. d) 7 de 25 o . e) El 5 es el número de personas cuyas edades se encuentran en cierto intervalo, y el 25 es el número del total de personas.

Respuestas. f) g) Es también la frecuencia relativa. Quiere decir que del total (que es igual a 1), hay 0.16 mujeres que tienen entre 40 y 49 años. h) Cuando las relaciones entre los datos se expresan en forma de porcentaje, el total es igual al 100%. El porcentaje de mujeres que tienen entre 40 y 49 años de edad es el 16%. i) Suman 1. j) En las 4 mujeres de 40 a 49 años, porque el número 4 en ese caso es la frecuencia; en cambio, en el otro caso se refiere al porcentaje, y en este ejemplo (el de las personas que asistieron a una reunión) el 4% equivale a una sola mujer. 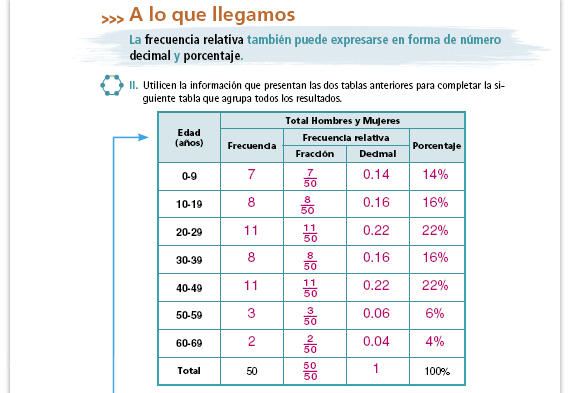Sugerencia didáctica. Cuando revisen sus respuestas deténgase un poco en el inciso g). Para algunos alumnos no es evidente que 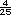y 0.16 son el mismo número.

Propósito de la actividad. Se pretende que los alumnos se den cuenta de los diferentes tipos de análisis que pueden hacerse al reorganizar la información.

Respuestas. a) 16% en total. b) Es igual, 4 hombres y 4 mujeres. Esta información la buscamos en las tablas anteriores, en las que se separó a hombres y mujeres. c) 1 d) 15 personas, que representan el 30%.

Sugerencia didáctica. Lean juntos esta información y pida a los alumnos que la copien en sus cuadernos.

Respuestas. 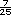a) El 30% sería equivalente a 9 corredores, por lo tanto, corresponde a 340 segundos. 0.1 como frecuencia relativa quiere decir que una décima parte de los corredores registró cierto tiempo (o el 10%). La décima parte del total de corredores (30) es 3, así que corresponde a los que hicieron 300, 350 y 360 segundos. 0.3 como frecuencia relativa puede expresarse también como el 30%, lo que equivale a 9 corredores (340 segundos). segundos). significa que tres de los treinta corredores registraron cierto tiempo, así que corresponde a 300, 350 y 360 segundos. Puede expresarse también como 0.1 o 10%. b) c) 10% (10 de 30).