Propósito de la sesión. Interpretar
información representada en gráficas
de barras y circulares de frecuencia
absoluta y relativa.
Organización del grupo. Para esta
sesión es conveniente que los
alumnos trabajen en parejas, excepto
en la sección Lo que aprendimos, que
es individual. |
Propósitos de la secuencia
Interpretar información representada en gráficas de barras y circulares de frecuencia absoluta y
relativa, proveniente de diarios o revistas y de otras fuentes. Comunicar información proveniente
de estudios sencillos, eligiendo la forma de representación más adecuada.
|
| Sesión |
Título y propósitos de la sesión |
Recursos |
Vínculos |
| 1 |
Qué dicen las gráficas
Interpretar información representada en
gráficas de barras y circulares de frecuencia
absoluta y relativa. |
|
|
| 2 |
Gráficas de barras
Elaborar e interpretar una gráfica de barras de
frecuencia relativa. |
|
Español I
Secuencia 10 |
| 3 |
Gráfica circular
Elaborar e interpretar una gráfica circular. |
Video
"El rating en la
televisión" |
Español I
Secuencia 14 |
| Sugerencia didáctica. Esta
información puede aprovecharse para
hablar sobre los censos, qué son y
para qué sirven. |
Propósito de la actividad. La
intención con la que se hacen las
preguntas del inciso a) es que
los alumnos analicen la gráfica y
sepan qué tipo de información es
la que proporciona y qué cosas no
pueden saberse por la manera en
que se organiza dicha información.
Permítales contestarlas sin darles aún
explicaciones.
Respuestas.
-
| a) |
La primera pregunta no puede
contestarse porque en el eje vertical
dice "número de personas", pero no
se sabe cuántas de esas personas
son niños. |
|
Respuestas
-
| a) |
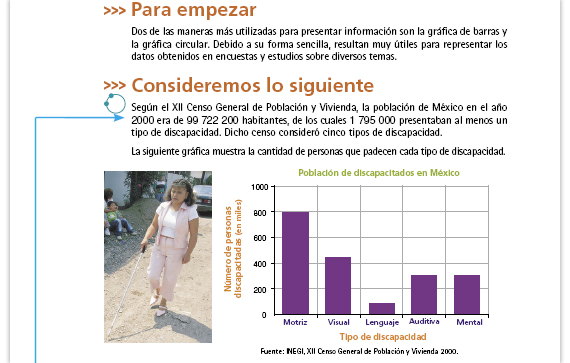
Son 5: Motriz, visual, lenguaje,
auditiva, mental. |
-
| b) |
La más frecuente es la motriz (es
la barra más alta en la gráfica). La
menos frecuente es la de lenguaje
(es la barra más corta en la
gráfica). |
-
| c) |
Es importante comentar esta
pregunta porque los alumnos
suelen cometer errores como
el que se plantea al analizar la
información contenida en gráficas
y tablas. En el eje vertical de la
gráfica dice "número de personas"
y también "en miles". Esto quiere
decir que el número al que llega
la altura de cada barra en la
gráfica debe multiplicarse por mil.
Los datos se escriben así para no
tener que poner muchos ceros en
los números de los ejes, lo cual
dificulta la lectura. Por lo tanto, no
hay 800 personas con discapacidad
motriz, sino 800 000. |
-
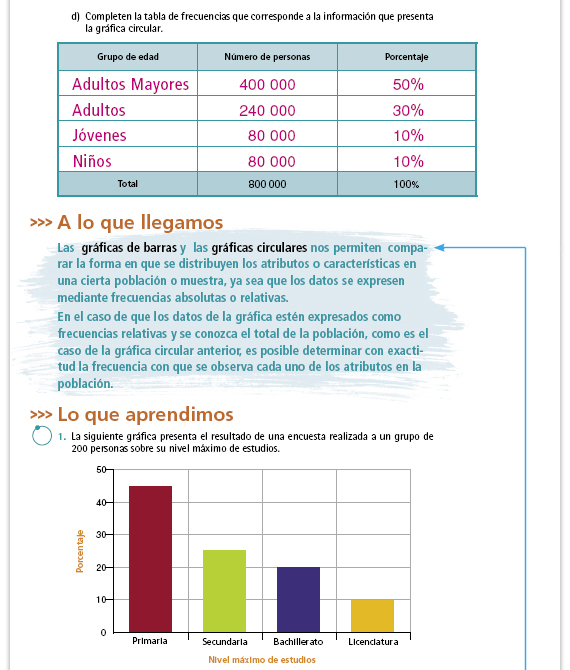
| d) |
Motriz, visual, auditiva y mental. |
-
| e) |
Hay 800 000 con discapacidad
motriz, y aproximadamente
450 000 con discapacidad visual,
85 000 con discapacidad de
lenguaje, 300 000 auditiva y
300 000 mental. El cálculo del
número de personas se hace por la
altura de la barra. Si es necesario
hay que medir. |
-
| f) |
No, aunque la suma de los datos
anteriores excede los 1 795 000,
el número total de personas con
alguna discapacidad no cambia, lo
que sucede es que hay personas
con más de una discapacidad. |
-
| g) |
Una persona puede tener más de
un tipo de discapacidad. |
|
 Propósito de la actividad.
Interpretar la información presentada
en una gráfica circular. Cada
sector representa un porcentaje, y
a diferencia de la gráfica anterior,
aquí sólo se consideran los datos
correspondientes a una de las
discapacidades (la motriz) y se
presenta información nueva: el grupo
de edad en el que se encuentran
quienes padecen tal discapacidad.
Propósito de la actividad.
Interpretar la información presentada
en una gráfica circular. Cada
sector representa un porcentaje, y
a diferencia de la gráfica anterior,
aquí sólo se consideran los datos
correspondientes a una de las
discapacidades (la motriz) y se
presenta información nueva: el grupo
de edad en el que se encuentran
quienes padecen tal discapacidad.
Respuestas.
-
-
| b) |
Adultos mayores, adultos,
jóvenes, niños. |
-
| c) |
Sí, de las personas con
discapacidad motriz, 10% son
niños y 10% son jóvenes, es decir
que hay la misma cantidad de
personas en cada grupo de edad
(80 000). |
|
 Sugerencia didáctica. Comenten
lo que aprendieron en la secuencia
anterior sobre la frecuencia absoluta
y relativa.
Sugerencia didáctica. Comenten
lo que aprendieron en la secuencia
anterior sobre la frecuencia absoluta
y relativa. |
Respuestas.
-
| a) |
Sugiérales que calculen el
porcentaje representado por
cada barra, si es necesario,
midiendo cada una. La suma de los
porcentajes debe ser 100%.
Las frecuencias relativas se
obtienen de la siguiente manera:
sabemos que la encuesta se realizó
a 200 personas. Los que cursaron
hasta primaria son el 45% de esos
200, es decir, 90 personas (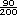 ), y
así con los demás valores. La tabla
debe mostrar los siguientes datos: ), y
así con los demás valores. La tabla
debe mostrar los siguientes datos: |
|
Frec. |
Frec. rel. |
Porc. |
| Prim. |
90 |
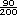 =0.45 =0.45 |
45% |
| Sec. |
50 |
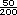 =0.25 =0.25 |
25% |
| Bach. |
40 |
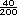 =0.2 =0.2 |
20% |
| Lic. |
20 |
 =0.1 =0.1 |
10% |
-
| b) |
La primera es incorrecta, sin
embargo, algunos alumnos podrían
pensar lo contrario porque en
la tabla se muestra que quienes
terminaron la licenciatura son el
10%, pero ese porcentaje está
referido al total de personas
encuestadas, que son 200, por lo
tanto, el 10% de 200 es 20.
La segunda también es
incorrecta. La suma de los
porcentajes de quienes tienen
como nivel máximo de estudios
la secundaria y los que tienen el
bachillerato es el 45%, lo que
equivale a 90 personas.
La tercera es correcta. El 45%
de las personas encuestadas
estudiaron hasta la primaria.
La cuarta es incorrecta. De
las personas encuestadas,
exactamente el 20% cursaron el
bachillerato.
|
|









 Propósito de la actividad.
Interpretar la información presentada
en una gráfica circular. Cada
sector representa un porcentaje, y
a diferencia de la gráfica anterior,
aquí sólo se consideran los datos
correspondientes a una de las
discapacidades (la motriz) y se
presenta información nueva: el grupo
de edad en el que se encuentran
quienes padecen tal discapacidad.
Propósito de la actividad.
Interpretar la información presentada
en una gráfica circular. Cada
sector representa un porcentaje, y
a diferencia de la gráfica anterior,
aquí sólo se consideran los datos
correspondientes a una de las
discapacidades (la motriz) y se
presenta información nueva: el grupo
de edad en el que se encuentran
quienes padecen tal discapacidad.
 Sugerencia didáctica. Comenten
lo que aprendieron en la secuencia
anterior sobre la frecuencia absoluta
y relativa.
Sugerencia didáctica. Comenten
lo que aprendieron en la secuencia
anterior sobre la frecuencia absoluta
y relativa.
 ), y
así con los demás valores. La tabla
debe mostrar los siguientes datos:
), y
así con los demás valores. La tabla
debe mostrar los siguientes datos: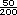 =0.25
=0.25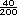 =0.2
=0.2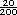 =0.1
=0.1