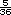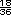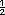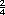|

|

|
 |
 |
Respuestas.
|

| Propósito de la sesión. Calcular
la probabilidad clásica de eventos
simples e interpretar la escala de la
probabilidad.
Organización del grupo. La sesión se trabaja en parejas y de manera individual. |

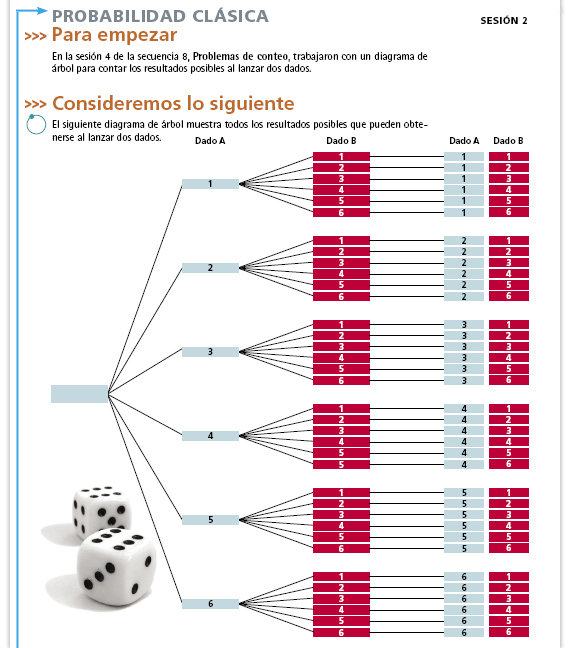
| Propósito de la pregunta. Lo
importante aquí es que los alumnos
lean y analicen el diagrama, las
probabilidades las calcularán después.
Respuestas. Una vez que hayan expresado sus opiniones, puede hacerles notar que un resultado mayor a 7 se obtiene de 15 distintas maneras, y que uno menor o igual a 7 se obtiene de 21 distintas maneras, por lo que no conviene apostar. Conviene apostar a obtener 7. No conviene apostar a obtener 2 o 12. |

Respuestas.
|

Respuestas.
|
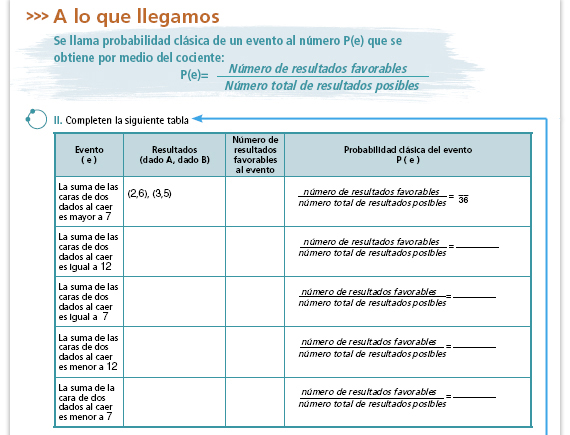
| Sugerencia didáctica. Si es posible, pida a los alumnos que también expresen la probabilidad con número decimal y mediante un porcentaje. |
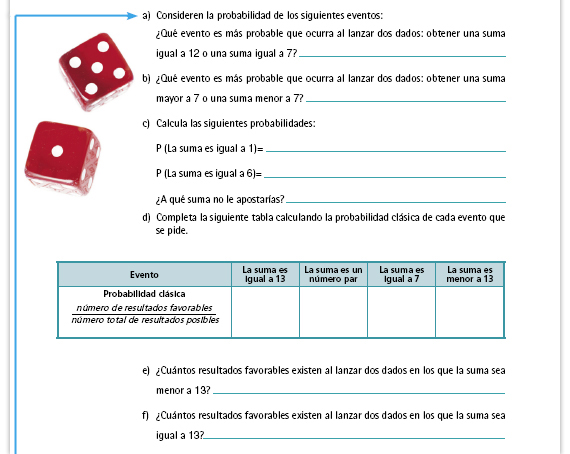
| Integrar al portafolios. Revise las
respuestas de los alumnos a los
incisos del a) al f). Si nota
dificultades, copie en el pizarrón la
tabla del número II de esta sección y
resuélvanla juntos.
Respuestas.
|

Sugerencia didáctica. Es importante
señalar la diferencia entre la
probabilidad frecuencial y la clásica.
Ambas se refieren a la probabilidad de
que un evento ocurra en situaciones
aleatorias, pero la frecuencial se
obtiene a partir de los resultados de
un experimento, y la clásica a partir
del análisis de la situación sin realizar
el experimento.
Sin embargo, se espera que cuando
un experimento se repita una gran
cantidad de veces, el valor de la
probabilidad frecuencial de un
evento se aproxime al valor de su
probabilidad clásica. Por ejemplo, el
valor de la probabilidad clásica de
"obtener una suma igual a 7" es 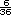 debido a que hay 6 de 36 formas de
obtenerla. Si lanzamos muchas veces
dos dados y reunimos los resultados,
el valor de probabilidad frecuencial de
obtener una suma igual a 7 debe de
aproximarse a
debido a que hay 6 de 36 formas de
obtenerla. Si lanzamos muchas veces
dos dados y reunimos los resultados,
el valor de probabilidad frecuencial de
obtener una suma igual a 7 debe de
aproximarse a 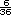 .
La notación utilizada es la misma en
ambos casos: P( e ). .
La notación utilizada es la misma en
ambos casos: P( e ). |

| Propósito del interactivo. Desarrollar una noción de probabilidad frecuencial al enumerar los posibles resultados de extraer canicas de una bolsa. Comparar las probabilidades clásicas con los datos experimentales. |

Respuestas.
|
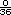 . La probabilidad de obtener
una suma igual a 6 es
. La probabilidad de obtener
una suma igual a 6 es