Propósitos de la sesión. Explorar la segunda potencia o el cuadrado de un número a partir de la obtención de la medida del lado de un cuadrado que mide un área determinada. Identificar la raíz cuadrada de un número A como el número que multiplicado por sí mismo da A. Identificar el cuadrado de un número y la raíz cuadrada como operaciones inversas. Organización del grupo. Se recomienda trabajar en parejas, a excepción del apartado Lo que aprendimos, que puede resolverse de manera individual. Materiales. Una calculadora por alumno o por pareja.

Eje

Sentido numérico y pensamiento algebraico.

Tema

Significado y uso de los números.

Antecedentes

Es la primera vez que los alumnos estudian estas operaciones; sin embargo, el contexto en el que se abordan (cálculo del área de cuadrados) es bastante conocido por ellos, lo que les permitirá hacer uso de sus conocimientos previos para iniciar el estudio de este tema.

Propósitos de la secuencia Resolver problemas que impliquen el cálculo de la raíz cuadrada y la potencia de exponente natural, ambas de números naturales y decimales.
Sesión	Título y propósitos de la sesión	Recursos
1	Cuadros y más cuadros Explorar la segunda potencia o el cuadrado de un número a partir de la obtención de la medida del lado de un cuadrado que mide un área determinada. Identificar la raíz cuadrada de un número A como el número que multiplicado por sí mismo da A. Identificar el cuadrado de un número y la raíz cuadrada como operaciones inversas.	Aula de medios "Cuadros y más cuadros" (Hoja de cálculo)
2	Cálculo de raíces cuadradas Calcular mediante aproximaciones la raíz cuadrada de un número que no es un cuadrado perfecto.	Video "Los babilonios y la raíz cuadrada" Interactivo "Método babilónico"
3	¿Cuántos tatarabuelos? Resolver problemas que impliquen el cálculo de las potencias de exponentes naturales de números naturales. Identificar la raíz cúbica de un número A como el número que tiene tercera potencia igual a A, y la raíz cuarta de un número A como el número que tiene cuarta potencia igual a A.	Interactivo "Diagrama de árbol"

Propósito de la actividad. Se les plantea el reto: ¿cuál será la medida del lado de un cuadrado cuya área es igual a 18 cm2? Dado que esa medida no es exacta, la tarea consiste en encontrar un número que multiplicado por sí mismo dé 18. Sugerencia didáctica. Respecto al inciso e), algunos alumnos podrían afirmar que no existe un cuadrado con esa área, pues con 4 cm obtienen 16 cm2 y con 5 cm, obtienen 25 cm2. Invítelos a probar utilizando también números decimales. Lo más probable es que prueben con varios números buscando aquel que más se aproxime a 18 cm2. Durante la comparación de resultados pida a los alumnos que identifiquen qué medida se acerca más al número buscado. Respuestas a) 4 cm2 (lado por lado = 2 × 2) b) 9 cm2 c) 4 cm d) 5 cm e) Sí existe, y la medida de sus lados es de 4.2426 cm aproximadamente.

Propósito de la actividad. Que los alumnos constaten que sí existe un cuadrado con esa superficie y que verifiquen la longitud de los lados midiendo. Respuestas. a) El cuadrado blanco tiene 6 cm por lado. Su área es de 36 cm2. Al trazar los cuatro triángulos azules pueden darse cuenta de que son triángulos rectángulos y son isósceles, y que su base y su altura miden 3 cm. También podrían considerar como base a la hipotenusa y medir la altura. b) El área de cada triángulo es de 4.5 cm2. c) El cuadrado azul está formado por los cuatro triángulos. Su área es de 18 cm2. d) La medida está entre 4.2 o 4.3 cm. Es importante que consideren que se trata de una aproximación. e) Si utilizan la medida de 4.2, el área es de 17.64 cm2, y si utilizan la medida de 4.3, el área es de 18.49 cm2. En el primer caso nos falta, en el segundo caso nos pasamos. Es decir que la medida real de cada lado debe ser un valor entre 4.2 y 4.3.

Sugerencia didáctica. El área del cuadrado azul es de 18 cm2; por lo tanto, sí existe un cuadrado con esa área. Pida a los alumnos que revisen lo que respondieron en el inciso e) del apartado Consideremos lo siguiente. Solicite a las parejas que registren en el pizarrón la medida que encontraron para los lados del cuadrado azul y el área que obtienen con esa medida (esto puede hacerse en una tabla que usted previamente puede trazar en el pizarrón). Pídales que identifiquen cuál es la medida que se aproxima más a la longitud del lado del cuadrado para que el área sea de 18 cm2.

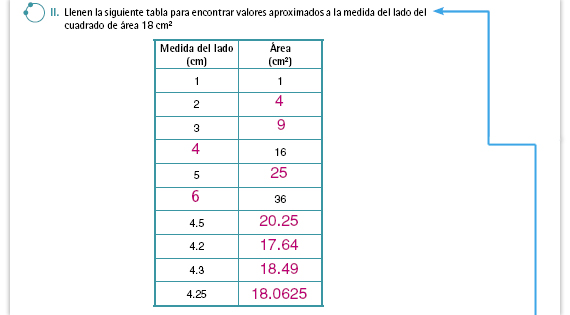
Propósito de la actividad. La tabla sirve para ir encontrando los valores del lado del cuadrado que hacen que el área se vaya aproximando a 18 cm2.

Respuestas. El valor de la tabla que más se aproxima es 18.0625, que corresponde a 4.25 cm por lado. Sin embargo, es posible hallar valores que se aproximen más a la medida buscada. Sugerencia didáctica. Pida a los alumnos que, con la ayuda de la calculadora, encuentren uno o dos valores que se aproximen más a la medida del lado. Usted puede hacerles notar que el valor debe estar entre 4.2 y 4.25; asimismo, puede comentarles que el valor exacto tiene una cantidad infinita de cifras decimales, por lo que siempre se toma una cantidad aproximada.

Sugerencia didáctica. Antes de que las parejas busquen la medida del lado del cuadrado, pida al grupo que estimen una respuesta. Algunas de esas estimaciones pueden ser registradas en el pizarrón para que después verifiquen qué tanto se acercaron a la respuesta.

Sugerencia didáctica. Se puede continuar la exploración hasta con tres cifras decimales. Los valores más aproximados son 5.65 y 5.66. Usted puede preguntar a todo el grupo si pueden decirle algunos números entre estos dos y cuáles de ellos son mejores opciones para la medida del lado. Los más aproximados son 5.656 y 5.657.

Pida a los alumnos que lean la información y que respondan en sus cuadernos las siguientes preguntas: -¿Cómo se calcula la segunda potencia o el cuadrado de un número? -¿Cómo se representa el cuadrado de un número? Dar algunos ejemplos. -¿Qué es la raíz cuadrada de un número? Dar ejemplos.

Sugerencia didáctica. Esta tabla puede servir para que los alumnos utilicen la tecla de la raíz cuadrada en la calculadora. También pueden ubicar la tecla que sirve para elevar al cuadrado y no sólo multiplicar a cada número por sí mismo.

Sugerencia didáctica. Pida a los alumnos que copien la información en sus cuadernos y que presenten ejemplos distintos a los que ahí se ofrecen. Además, usted puede recordarles las operaciones inversas que ya conocen: suma y resta, multiplicación y división.

Integrar al portafolios. Respuesta. 1. Si consideran hasta con dos cifras decimales, es 1.41, si consideran cuatro cifras decimales, es 1.4142; pida a los alumnos que registren las distintas operaciones que efectuaron, ya sea que las hayan hecho con calculadora o con lápiz y papel.