
|

|

|
 |
 |

| Propósito de la sesión. Calcular la
raíz cuadrada de un número dado.
Organización del grupo. Se proponen tres formas de trabajo: el apartado Para empezar puede trabajarse en forma grupal, el apartado Consideremos lo siguiente en parejas, y los apartados Manos a la obra y Lo que aprendimos de manera individual. Materiales. Calculadora. |

| Propósito de la actividad. Presentar a los alumnos un procedimiento para calcular la raíz cuadrada de un número, en el contexto del área de un cuadrado: al calcular la raíz cuadrada de un número estamos buscando la medida del lado de un cuadrado del que se conoce el área. |

| Propósito del video. Visualizar la aplicación del método babilónico en el cálculo de raíces cuadradas de distintos números. |

| Sugerencia didáctica. Antes de revisar cada uno de los pasos del método babilónico, comente al grupo que se va a buscar la medida del lado de un cuadrado cuya área es de 32 cm2. Pida al grupo que haga una estimación de la posible medida del lado del cuadrado (la respuesta es entre 5 y 6 cm). Posteriormente, una vez que hayan revisado el método babilónico, tendrán oportunidad de verificar su respuesta. |
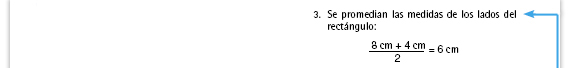
| Propósito de la actividad. El
método de los babilonios considera un
rectángulo con un área determinada,
al cual gradualmente se modifican las
medidas de sus lados -conservando el
área-, de manera tal que cada vez se
acerca más a un cuadrado.
Sugerencia didáctica. Si lo considera necesario, recuerde a los alumnos que el procedimiento para encontrar un promedio (paso número 3) consiste en sumar los valores y luego dividir esa suma entre el número de valores que se están promediando. |

| Respuesta. Se divide 32 entre 6. Es igual a 5.333333... Si se toman sólo dos cifras decimales, es 5.33. |

| Sugerencia didáctica. Usted puede
pedir a los alumnos que resuelvan la
ecuación que se les plantea:
6x = 32 x = 32 ÷ 6 x = 5.333 |
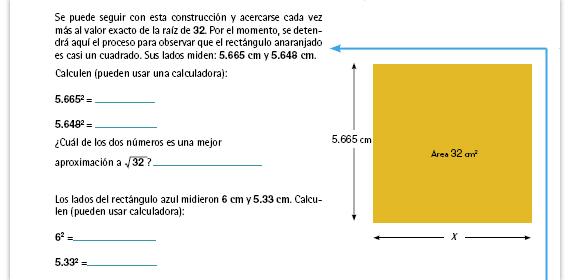
| Respuestas. Se obtiene:
5.6652 = 32.092225 5.6482 = 31.899904 El primer número es el que más se acerca a la raíz cuadrada de 32. |

| Respuesta. El rectángulo anaranjado
es el que más se aproxima.
Sugerencia didáctica. Entre todo el grupo pueden realizar una aproximación más si se promedia 5.665 y 5.648. |

| Sugerencia didáctica. Mientras las parejas resuelven, procure estar pendiente de cómo lo hacen y apóyelos si tienen dificultades. Particularmente, sugiérales que revisen nuevamente cada uno de los pasos que se describen en el caso anterior. |

| Respuesta. Aproximadamente 2.701
Sugerencia didáctica. Usted puede pedir a algunas parejas que vayan indicando las medidas de los lados de cada uno de los rectángulos que encontraron. |

| Propósito de la actividad. Que de manera individual, los alumnos ejerciten el método babilónico para obtener la raíz cuadrada de un número. Los alumnos pueden recurrir a los ejercicios anteriores en caso de que tengan dudas o dificultades para resolver este ejercicio. |

| Propósito del interactivo. Obtener la aproximación de la raíz cuadrada de un número por medio del método babilónico. |

| Sugerencia didáctica. En cada uno
de los pasos siguientes usted puede
pedirles que dibujen los rectángulos en
sus cuadernos.
Respuestas. 2.862 = 8.1796 3.52 = 12.25 |

| Respuesta. Una buena aproximación con cuatro cifras decimales es 3.1622. |

| Sugerencia didáctica. Puede pedir a algunos alumnos que encuentren todavía una o dos aproximaciones mejores. Esto debe hacerse utilizando más cifras decimales en los resultados. |

| Integrar al portafolios.
Si identifica que los alumnos aún
tienen dificultades para encontrar
la raíz cuadrada de un número
con el método babilónico, revise
con ellos cada uno de los pasos
tomando este caso como ejemplo.
Recuerde que no se trata de que los
alumnos sean expertos en el manejo
de este método, pues hay otros
recursos, como la calculadora, que
en ciertas circunstancias permiten
obtener resultados de manera más
rápida y segura; el propósito es que
comprendan qué implica buscar la raíz
cuadrada de un número.
Respuesta. El primer rectángulo puede ser de 3 × 6. Una buena aproximación es 4.2426. |

Respuestas.
|