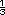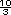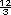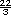|

|

|
 |
 |

| Propósito de la sesión. Analizar
y representar algebraicamente la
relación de dependencia en una
relación funcional de la forma y =
ax.
Organización del grupo. Se sugiere trabajar la sesión en parejas, excepto en la sección Lo que aprendimos y en momentos de discusión grupal. |
| Eje |
| Sentido numérico y pensamiento algebraico. |
| Tema |
| Significado y uso de las literales. |
| Antecedentes |
| En secuencias anteriores los alumnos han expresado algebraicamente reglas de sucesiones numéricas y fórmulas geométricas. En esta secuencia van a expresar algebraicamente relaciones entre dos cantidades que varían. |
| Propósitos de la secuencia
Analizar en situaciones problemáticas la presencia de cantidades relacionadas y representar esta relación mediante una tabla y una expresión algebraica. |
||
| Sesión | Propósitos de la sesión | Recursos |
| 1 | La expansión del universo
Analizar y representar algebraicamente la relación de
dependencia en una relación funcional de la forma y = ax.
|
Video "La expansión del universo" |
| 2 | Los husos horarios
Analizar y representar algebraicamente la relación de
dependencia en una relación funcional de la forma y = x + ab.
|
|
| 3 | Cocina navideña
Analizar y representar algebraicamente la relación de
dependencia en una relación funcional de la forma y = ax + b.
|
Aula de medios "Cocina navideña" (Hoja de cálculo) |
| 4 | El recibo de teléfono
Identificar la expresión algebraica correspondiente a una
relación funcional de la forma y = a(x - b) + c.
|
|

| Propósito del video. Introducir las ideas generales de la ley de Hubble: Velocidad de alejamiento de una galaxia y Constante de Hubble. |

 Propósito de la actividad. En otras
secuencias los alumnos han trabajado
con cantidades directamente
proporcionales. Lo que aprendieron
les permitirá contestar con relativa
facilidad los incisos a) y b); sin
embargo, lo que pretende constituirse
en un reto en esta sesión es el inciso
c), que es expresar algebraicamente la
relación entre las cantidades.
Quizá los alumnos tengan dificultades
para lograr una expresión correcta.
Si es el caso, no los corrija ni les dé
la solución, permítales continuar
resolviendo.
Propósito de la actividad. En otras
secuencias los alumnos han trabajado
con cantidades directamente
proporcionales. Lo que aprendieron
les permitirá contestar con relativa
facilidad los incisos a) y b); sin
embargo, lo que pretende constituirse
en un reto en esta sesión es el inciso
c), que es expresar algebraicamente la
relación entre las cantidades.
Quizá los alumnos tengan dificultades
para lograr una expresión correcta.
Si es el caso, no los corrija ni les dé
la solución, permítales continuar
resolviendo.
Respuestas.
|
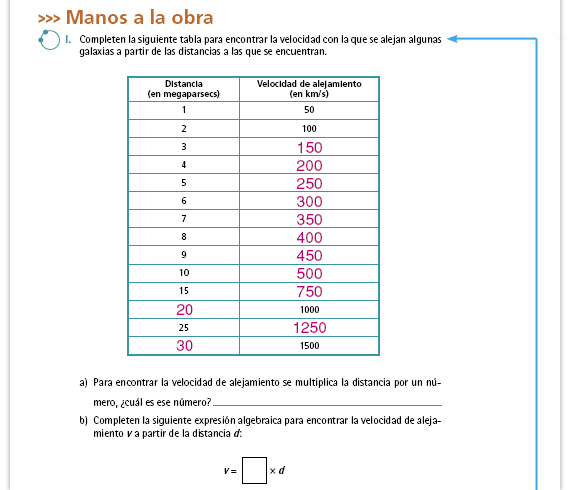
Respuestas. Para hallar los datos
faltantes se multiplica la distancia
por 50. Si se conoce la velocidad,
se divide ésta entre 50.
|

 Sugerencia didáctica. En este
momento puede ser útil recordar
el concepto de constante de
proporcionalidad que los alumnos
trabajaron en la secuencia 15.
Sugerencia didáctica. En este
momento puede ser útil recordar
el concepto de constante de
proporcionalidad que los alumnos
trabajaron en la secuencia 15.
Respuestas. La constante de proporcionalidad que se busca permite encontrar la velocidad de alejamiento a partir de la distancia. Por ejemplo, para obtener la velocidad de alejamiento de una galaxia que está a 3 megaparsecs se multiplica por el número 50 y se obtiene que la velocidad es 150 km/s. El número 50 corresponde a la constante de proporcionalidad. |

Respuestas.
v = 50 × d
|

Respuestas.
|

| Posibles dificultades. Es común
que los alumnos vean las fórmulas
v = 50d y d = v ÷ 50
como expresiones que no están
relacionadas, y por consiguiente,
se las aprendan de manera separada.
Analice con ellos ambas fórmulas
para que puedan relacionarlas.
Sugerencia didáctica. Escriba en el pizarrón la expresión que permite encontrar la velocidad conociendo la distancia (v = 50d ) y la que permite hallar la distancia conociendo la velocidad de alejamiento (d = v ÷ 50) y analícenlas. Propongan distintas variables (tanto velocidades de alejamiento como distancia) y utilicen las expresiones algebraicas para hallar la otra variable. Pregunte a los alumnos en qué se parecen y en qué son distintas las dos expresiones y si creen que están relacionadas o no. |

| Integrar al portafolios. Pida a los
alumnos una copia de sus respuestas a
las actividades de esta sección.
Respuestas.
|
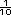 megaparsecs).
megaparsecs).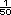 megaparsecs).
megaparsecs).