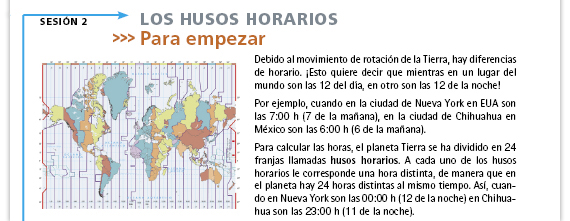
Propósito de la sesión. Analizar y representar algebraicamente la relación de dependencia en una relación funcional de la forma y = x + ab. Organización del grupo. En la sesión hay trabajo individual, en parejas y en equipo.

Sugerencia didáctica. Puede aprovechar esta actividad para comentar con los alumnos sobre las distintas maneras de escribir la hora. Por ejemplo: -Después de la medianoche viene la 1 de la mañana, las 2, 3, etc. Después del mediodía viene la 1 de la tarde, las 2, 3... hasta llegar nuevamente a la medianoche. -En vez de decir "1 de la mañana" también suele decirse "1 a.m.". Las letras "a.m." significan "antes del meridiano", es decir, antes del mediodía. Después del mediodía se dice "p.m." que significa "pasado meridiano". -También se cuentan las horas empezando en las 0:00 h (medianoche). Se va aumentando de una en una hasta las 23:00 h, y la que sigue es otra vez las 0:00 h. Por eso, después de las 12 de la tarde siguen las 13:00 h (la 1 de la tarde), las 14:00 h (las 2 de la tarde), y así sucesivamente.

Propósito de la actividad. La intención es que al llegar al inciso c) los alumnos expresen algebraicamente la relación entre la hora de Chihuahua y la hora de Nueva York. Déles tiempo para trabajar la situación y no les proporcione la respuesta. Respuestas. Para conocer la hora de Nueva York hay que aumentar una hora a la de Chihuahua. a) Las 16:00 h b) A partir de las 15:45 de Chihuahua. El papá sale a las 15:00 h (hora de Nueva York), y tras 1 hora y 45 minutos de trayecto, llega a su casa a las 16:45 (de Nueva York), que son las 15:45 de Chihuahua. c) De las 4:15 de la mañana a las 15:45 (hora de Chihuahua), tomando en cuenta los trayectos de ida y vuelta.

Posibles dificultades. Los estudiantes podrían sentirse confundidos porque la expresión y = x + 1 no permite encontrar la hora de Nueva York. Explíqueles que cuando se usa esta expresión se pasa de las 24:00 h y que, pasadas las 24:00 h se reinicia el conteo de horas. Por ejemplo, en lugar de ser las 24:30, en Nueva York son las 00:30. En el inciso a) es posible que digan que la operación que se hace es sumar 1 y quitarle el 24. Eso es correcto, pero no es una operación algebraica. No los corrija, y permítales pasar al inciso b). En el inciso b) necesitarán interpretar el "quitarle el 24" como un resto 24. Si no surge en el grupo, dígaselos. Al final, los alumnos deberán conjugar esta última observación con el sumar 1 y así obtener: y = x - 23.

Respuestas. La hora de Los Ángeles es igual a la hora de Chihuahua menos 2. La hora de Tokio es igual a la hora en Chihuahua más 15. a) Las 18:00 h. b) Las 17:00 h. c) y = x - 2 d) i) z = x + 15 ii) z = x - 9

Respuestas. a) 22:00 h b) 1:00 h. c) 0:00 h. d) 9:00 h.

Respuestas. a) z (la hora de Tokio) y x (la hora de Chihuahua). b) 15 (las horas de diferencia entre Chihuahua y Tokio).

Propósito de la actividad. Se espera que completar la tabla no sea difícil para los alumnos, el reto consiste en la escritura de las expresiones algebraicas. Integrar al portafolios. Solicite a los alumnos una copia de sus respuestas a las actividades del número 1. Posibles dificultades. Es común que los alumnos piensen que si se cambia la letra que representa a una variable la expresión será incorrecta. Es importante que los alumnos sepan que se pueden poner letras distintas, siempre y cuando esté claro qué representa cada una. Usted puede escribir en el pizarrón las expresiones que hayan elaborado y cambiarles las letras para que ellos digan si es correcto o no. Respuestas. a) (r es Rocío, j es Juan, f es Fernanda y l es Luis). Rocío: r = l + 4 Juan: j = l +2 Fernanda: f = l - 5 c) r, j, f y l (o las letras que ellos hayan usado). d) 4, 2 y 5.

Respuestas. a) 5 cm b) 9 cm c) a = b - 3 d) a y b e) 3 Posibles dificultades. Los alumnos podrían pensar que la expresión algebraica es a = b + 3, porque saben que la base es 3 cm mayor que la altura. Revise sus respuestas y si cometieron ese error pídales que la utilicen con los valores de los incisos a) y b) para que comprueben si es correcta.