Propósito de la sesión. Analizar y representar algebraicamente la relación de dependencia en una relación funcional de la forma y = ax + b. Organización del grupo. La sesión se trabaja en parejas, habiendo momentos de discusión grupal.

Propósito de la actividad. Al igual que en la sesión anterior, lo que se pretende es que los alumnos escriban expresiones algebraicas que les permitan modelar la situación y encontrar los valores de las variables. Respuestas. a) 165 minutos. b) 210 minutos. c) 187.5 minutos. d) Siendo t el tiempo de horneado (en minutos) y p el peso del pavo (en kilos), t = 15p + 90 Se leería "tiempo de horneado es igual a peso por 15 más 90".

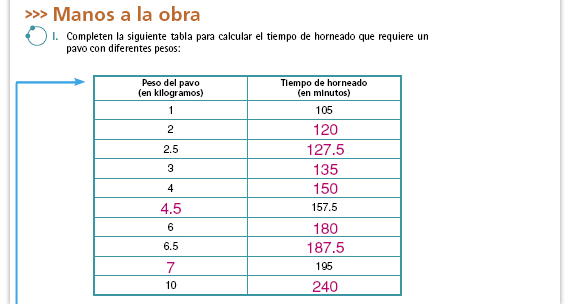
Posibles respuestas. Para responder el inciso d) los alumnos podrían escribir cosas como "Se multiplica el peso por 15 y al resultado se le suma 90", que si bien son correctas, no son expresiones algebraicas. Permítales esas respuestas siempre y cuando sean correctas, y cuando terminen de resolver la sección Manos a la obra dígales que las expresen algebraicamente.

Respuestas. Cuando se conoce el peso, se multiplica éste por 15 y se le suma 90. Cuando se conoce el tiempo de horneado, se le resta 90 y se divide entre 15. Posibles dificultades. La expresión (algebraica o no) que los alumnos escribieron en la sección anterior funciona para cuando se quiere hallar el tiempo de horneado conociendo el peso del pavo. Sin embargo, en la tabla se les plantea también el caso inverso: averiguar el peso del pavo conociendo el tiempo de horneado. Si lo cree conveniente, repasen juntos la expresión original t = 15p + 90 (o equivalentes), y analicen de qué manera podrían averiguar el peso. Puede preguntarles: "Si sabemos que el tiempo de horneado es de 105 minutos, ¿cómo pueden estar seguros de que el pavo pesa 1 kg?". Trabajar con valores que ya conocen para las variables puede ser de ayuda para resolver la cuestión. Otra dificultad que está asociada a lo anterior es la de desconocer en qué orden deben hacerse las operaciones. Saben que el tiempo de horneado es igual al peso por 15 más 90, pero conociendo el tiempo de horneado ¿qué debe hacerse primero, restar los 90 minutos o dividir entre 15? Si los alumnos tuvieran esa duda, repasen juntos la expresión que escribieron antes. Sugerencia didáctica. Cuando terminen de llenar la tabla, pida a los alumnos que expresen los tiempos de horneado en horas, minutos y segundos, especialmente en los casos en que el resultado es un número como 157.5 minutos.

Respuestas. a) 15 b) 90 c) t = 15p + 90

Respuestas. a) El tiempo de horneado t y el peso del pavo p. b) 15 y 90

Integrar al portafolios. Guarde las respuestas de los alumnos a la actividad III y valórelas para ver si han comprendido.

Respuestas. a) Necesita 90 minutos más, porque la diferencia es de 6 kg, entonces 6 × 15 = 90. b) No es cierto, hay que tener en cuenta la otra constante: añadir 90 minutos al tiempo de horneado. Esto puede verse en el ejemplo anterior, mientras que para el pavo de 3 kg el tiempo de horneado es de 135 minutos, para el de 9 kg es de 225 minutos. 9 es el triple de 3, pero el tiempo de horneado no es el triple.

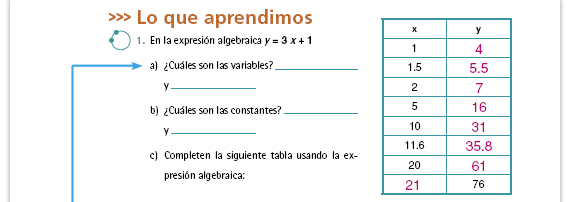
Posibles dificultades. Es un error común confundir una constante (multiplicativa) con una constante aditiva. Sugiera a los alumnos que lean con cuidado las dos expresiones algebraicas para que analicen qué es lo que hacen el 80 y el 16 en cada caso. En la primera el tiempo de horneado se obtiene así: cada kilo de pavo se multiplica por 80 minutos y luego se añaden 16 minutos. Aquí el 80 es una constante (se multiplica) y el 16 es una constante aditiva (se suma). En la segunda el tiempo de horneado se obtiene de esta manera: cada kilo de pavo se multiplica por 16 y luego se añaden 80 minutos. Aquí el 16 es una constante (se multiplica) y el 80 es una constante aditiva (se suma). Esta es la expresión correcta. Si los alumnos no notan la diferencia o tienen dificultades para elegir la expresión correcta, pídales que calculen el tiempo de horneado de un pavo de 7 kg a partir de la receta y luego, utilizando cada una de las expresiones algebraicas.

Respuestas. a) y, x . b) 3, 1. c) x se multiplica por 3 y se suma 1. Para hallar el valor de x cuando y es igual a 76 deben realizarse las operaciones inversas y en orden contrario: primero restar 1 y luego dividir entre 3, o bien, plantear la ecuación 3x + 1 = 76 y resolverla.