
|

|

|
 |
 |

| Propósito de la sesión.
Trazar un círculo,
dados dos puntos. Identificar cuántos
círculos se pueden trazar bajo esas
condiciones.
Organización del grupo. Se sugiere que la sesión se trabaje en parejas. Materiales. Regla y compás. |
| Eje |
| Forma, espacio y medida. |
| Tema |
| Formas geométricas. |
| Antecedentes |
| En la escuela primaria los alumnos aprendieron a construir círculos a partir de la medida del radio. Asimismo, aprendieron a ubicar el centro de una circunferencia utilizando dos recursos: por medio del punto en el que se cruzan los ejes de simetría, y mediante el trazo de perpendiculares de cuerdas no paralelas. En esta secuencia aprenderán otras formas de construir círculos, y para ello requerirán apoyarse en el trazo de mediatrices que trabajaron en la secuencia 12. |
| Propósitos de la secuencia
Construir círculos que cumplan condiciones dadas a partir de diferentes datos. |
||
| Sesión | Propósitos de la sesión | Recursos |
| 1 | Las circunferencias que pasan por dos puntos Trazar un círculo, dados dos puntos. Identificar cuántos círculos se pueden trazar bajo esas condiciones. | Video "Las circunferencias que pasan por dos puntos" |
| 2 | Cuerdas y circunferencias Identificar en qué casos es posible trazar un círculo dadas dos cuerdas. | Interactivo "Construcción de circunferencias" |
| 3 | Tres puntos y una circunferencia Identificar en qué casos es posible trazar un círculo dados tres puntos. | Interactivo "Construcción de circunferencias con la mediatriz" Aula de medios "Tres puntos y una circunferencia" (Geometría dinámica) |
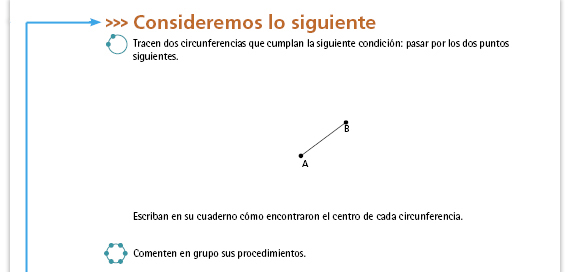
Propósito de la actividad. Hay dos
aspectos centrales en la resolución de este
problema:
Sugerencia didáctica. Si lo considera necesario, aclare a los alumnos que el pasar por los dos puntos no significa tomar uno como centro y al otro como radio, sino que ambos puntos deben ser parte de la circunferencia. Posibles procedimientos. Una forma de resolver es por ensayo y error, esto es, abrir el compás haciendo una estimación del radio, probar si con ese radio es posible trazar una circunferencia que pase por los dos puntos. Si no es así, cerrar o abrir más el compás, según lo requieran, hasta aproximarse lo más posible a la circunferencia buscada. El trazo de la segunda circunferencia podría llevarse a cabo de la misma manera. Una forma más sistemática de trazar la primera circunferencia es la que se presenta en la actividad II del apartado Manos a la obra. La segunda circunferencia puede resultarles más complicada de encontrar, pues necesitan situar un punto que esté a la misma distancia de los puntos A y B. Esto puede hacerse trazando la mediatriz que ya estudiaron en la secuencia 12, pero es posible que pocos alumnos recurran a ello. |
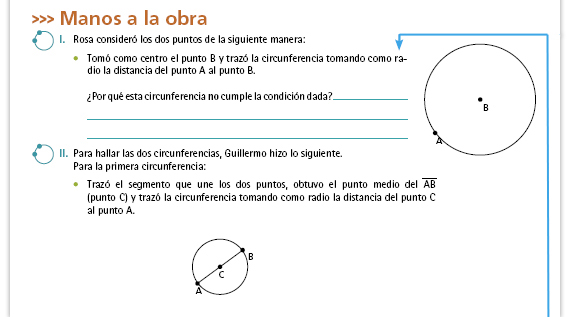
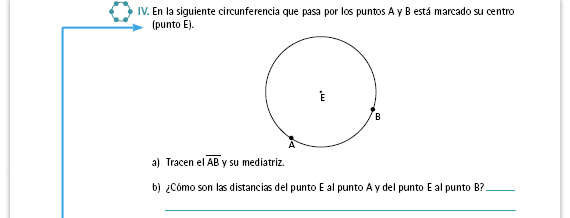
| Respuesta. Porque no pasa por el punto B, pues se tomó a éste como centro. |

| Respuestas. Las medidas de las distancias en ambos incisos son las mismas, AC = BC. |
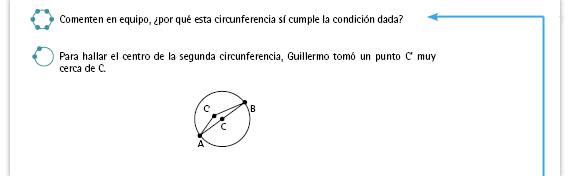
Sugerencia didáctica. Pida a algunas
parejas que comenten sus respuestas
al grupo. Además de que los alumnos
lleguen a concluir que en este caso
la circunferencia sí pasa por los dos
puntos, enfatice las ideas que se
sugieren en seguida para enriquecer
los argumentos de los alumnos:
|

Respuestas. Las medidas de las
distancias en ambos incisos no son
las mismas: AC´ 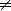 BC´. BC´. |

Sugerencia didáctica. Una vez que
los alumnos hayan expresado sus
argumentos, enfatice lo siguiente:
|

Propósito de la actividad. Se espera
que los alumnos:
Sugerencia didáctica. Si lo considera necesario, pida a los alumnos que revisen la secuencia 12 para que recuerden el procedimiento para trazar la mediatriz. |

| Respuestas. Las distancias de A y B al punto E son las mismas: AE=BE. Las distancias de A y B al punto F son las mismas: AF=BF. |

| Respuesta. La distancia de los nuevos puntos sobre la mediatriz hacia A y B es la misma (aunque diferente a las del inciso f). |
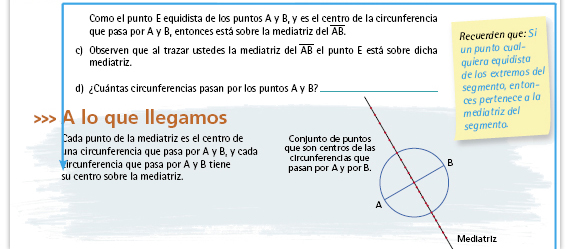
| Propósito de la actividad. Que los alumnos identifiquen que cualquier punto de la mediatriz es el centro de una circunferencia que pasa por los puntos A y B; por lo tanto, pueden trazarse distintas circunferencias que pasen por los puntos A y B, y el centro de cada una de ellas siempre será un punto de la mediatriz. |
| Integrar al portafolios. Solicite a los alumnos que tracen dos puntos cualesquiera (puntos P y Q), y que tracen dos circunferencias que pasen por esos dos puntos. Si identifica que los alumnos tienen dificultades, repase con ellos la actividad III del apartado Manos a la obra. |

| Propósito del video. Visualizar la construcción de la familia de circunferencias que pasan por los extremos de un segmento dado. |
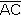 y
y 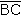 son radios
de la circunferencia.
son radios
de la circunferencia.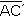 y
y 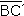 tienen
medidas distintas.
tienen
medidas distintas.