
|

|

|
 |
 |

| Propósito de la sesión. Identificar en
qué casos es posible trazar un círculo
dadas dos cuerdas.
Organización del grupo. Se sugiere que los alumnos trabajen en parejas durante toda la sesión. Materiales. Regla y compás. |
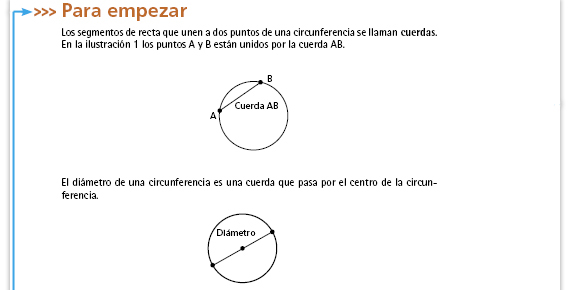
| Sugerencia didáctica. Es importante que lea y comente esta información con los alumnos, pues se les presenta un nuevo término que deberán incorporar a su vocabulario matemático. Puede pedir a una pareja de alumnos que elabore un cartel con esta información para que esté a la vista de todo el grupo. |
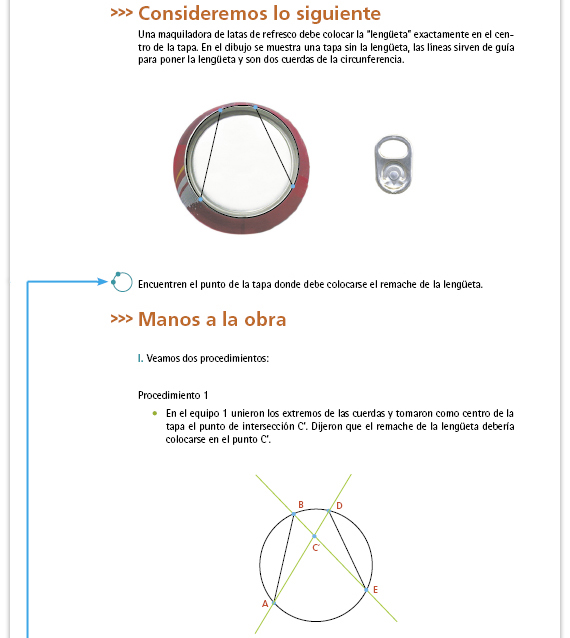
| Posibles procedimientos.
Algunos
alumnos podrían tratar de ubicar el
centro de la circunferencia "a ojo",
trazando dos "diámetros" que se
corten perpendicularmente. Si es así,
pregunte a esos alumnos cómo pueden
estar seguros de que ese es el centro,
y pregúnteles si las dos cuerdas que se
indican en el dibujo podrían servirles
de algo para encontrar el centro de la
circunferencia.
Otra forma más sistemática de resolver, es trazar la mediatriz de cada una de las cuerdas; el punto en el que se cruzan las mediatrices es el centro de la circunferencia, y es donde debe colocarse el remache. |

Sugerencia didáctica. Una vez que
los alumnos hayan expresado sus
argumentos, subraye lo siguiente:
En cambio, en el procedimiento 2, cualquier punto de cada mediatriz equidista de los extremos del segmento correspondiente, y el punto de intersección de las mediatrices equidista de los cuatro extremos; por lo tanto, los segmentos 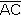 , ,
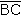 , ,
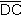 y y
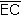 son radios de la circunferencia. Los
alumnos pueden comprobarlo trazando
la circunferencia tomando como centro
el punto C y como radio cualquiera de
los cuatro puntos (A, B, D, E). son radios de la circunferencia. Los
alumnos pueden comprobarlo trazando
la circunferencia tomando como centro
el punto C y como radio cualquiera de
los cuatro puntos (A, B, D, E). |
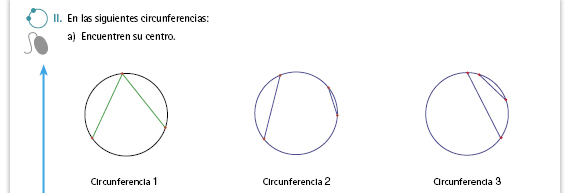
| Propósito del interactivo. Mostrar los casos posibles para construir una circunferencia. |
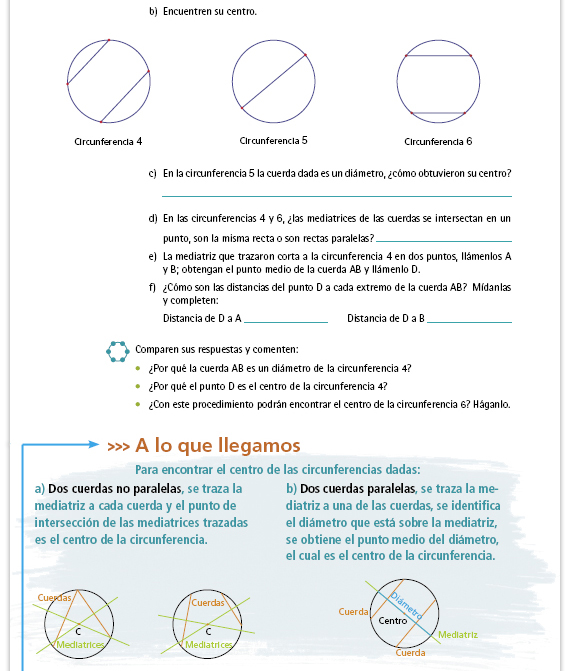
 Pida a una pareja de alumnos que
elabore un cartel con esta información
y que lo pegue en el salón de clases.
Los alumnos pueden copiar esta
información en sus cuadernos e
ilustrarla con ejemplos.
Pida a una pareja de alumnos que
elabore un cartel con esta información
y que lo pegue en el salón de clases.
Los alumnos pueden copiar esta
información en sus cuadernos e
ilustrarla con ejemplos. |
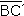 ,
,
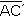 ,
,
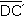 y
y
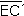 tendrían la misma
medida, y serían radios de la
circunferencia.
tendrían la misma
medida, y serían radios de la
circunferencia.