Propósito de la sesión. Identificar en qué casos es posible trazar un círculo dados tres puntos. Organización del grupo. Se recomienda trabajar la sesión en parejas; si lo considera conveniente, el apartado Lo que aprendimos puede resolverse de manera individual. Materiales. Regla y compás.

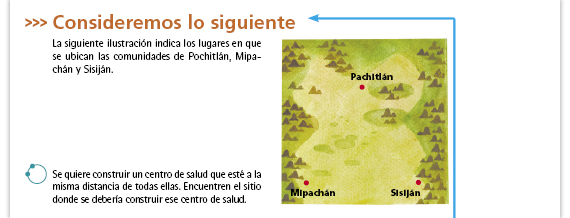
Posibles procedimientos. Los alumnos resolvieron un problema similar en la sesión 3 de la secuencia 12, por lo que es posible que utilicen el mismo procedimiento que usaron en aquel problema: unir los tres puntos mediante segmentos, trazar la mediatriz de cada segmento y ubicar al punto en el que se cortan las mediatrices como el lugar donde debe construirse el Centro de Salud. Otra forma en que los alumnos podrían plantear el problema, aunque también utilicen las mediatrices para resolverlo, es trazando segmentos que representan las cuerdas de una circunferencia. Lo que deben buscar es el centro de esa circunferencia.

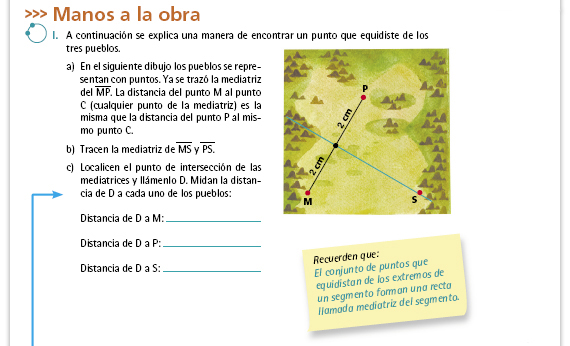
Respuesta. La distancia es la misma en los tres casos.

Respuesta. Es suficiente el trazo de dos mediatrices.

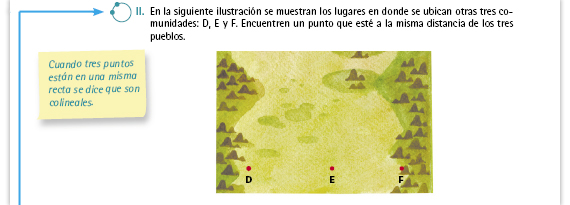
Propósito de la actividad. Que los alumnos identifiquen en qué casos no es posible trazar una circunferencia dados tres puntos, y esto es cuando los puntos no son colineales. Es importante que los alumnos logren expresar las razones por las cuales no puede trazarse la circunferencia en ese caso.

Respuesta. No hay intersección porque las mediatrices son líneas paralelas.

Respuestas. a) No se intersecan porque son paralelas. b) Dado que las mediatrices no se intersecan, no es posible ubicar un punto que esté a la misma distancia de los tres pueblos. En todo caso, el lugar más conveniente para establecer el centro de salud sería a la mitad del segmento .

Sugerencia didáctica. Pida a los alumnos que copien esta información y que hagan trazos que ilustren cada uno de los casos.

Integrar al portafolios. Sólo en el caso 2 no es posible trazar la circunferencia, pues los tres puntos son colineales. En los casos 1 y 3 se le muestran a usted las tres mediatrices, pero los alumnos podrían trazar sólo dos de ellas, lo cual es correcto. Si identifica que los alumnos tienen algunas dificultades con el caso 2 (por ejemplo, considerar erróneamente el punto E como el centro de la circunferencia), revise nuevamente con ellos la actividad II del apartado Manos a la obra y comente con ellos el apartado A lo que llegamos de esta sesión. Si identifica que tienen dificultades con los casos 1 y 3, revise con los alumnos nuevamente la actividad I de ese mismo apartado.

Propósito del interactivo. Mostrar la construcción de la circunferencia.