Propósito de la sesión. Determinar el número como la razón entre la longitud de la circunferencia y el diámetro. Resolver problemas de proporcionalidad que implican el cálculo del perímetro del círculo. Organización del grupo. Los alumnos pueden trabajar en parejas, a excepción del apartado Lo que aprendimos, que puede resolverse de manera individual. Materiales. Calculadora, regla, compás, tijeras y hojas blancas.

Eje

Forma, espacio y medida.

Tema

Medida.

Antecedentes

En la escuela primaria los alumnos identificaron el número como el número de veces que el diámetro cabe en la circunferencia; asimismo, aprendieron a calcular el perímetro de un círculo aplicando la fórmula. En este grado de la educación secundaria profundizaran en el estudio de la relación que existe entre la circunferencia y el diámetro en diversas situaciones problemáticas.

Propósitos de la secuencia Determinar el número como la razón entre la longitud de la circunferencia y el diámetro. Justificar y usar la fórmula para el cálculo de la longitud de la circunferencia.
Sesión	Propósitos de la sesión	Recursos
1	La relación entre circunferencia y diámetro Determinar el número como la razón entre la longitud de la circunferencia y el diámetro. Resolver problemas de proporcionalidad que implican el cálculo del perímetro del círculo.	Video "Relación entre circunferencia y diámetro" Interactivo "¿De dónde salió Pi?" "El número Pi"
2	Perímetro del círculo Obtener una fórmula para calcular el perímetro del círculo. Resolver problemas de proporcionalidad que implican al número y a la fórmula del perímetro de un círculo. Resolver problemas de proporcionalidad que implican al número y a la fórmula del perímetro de un círculo.	Video "Temperaturas ambientales" Interactivo "Temperaturas"

Propósitos de la actividad. Que los alumnos obtengan el perímetro de los círculos haciendo uso de recursos distintos a la utilización de la fórmula. Que identifiquen cuántas veces cabe el diámetro en la circunferencia. Sugerencia didáctica. Es posible que al girar los círculos sobre la regla haya algunas dificultades para medir su perímetro de manera exacta; por ello, pida a los alumnos que lo hagan lo más cuidadosamente posible y que utilicen medidas aproximadas.

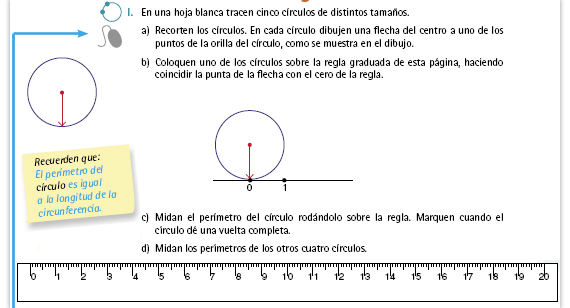
Propósito del interactivo. Justificar el valor de .

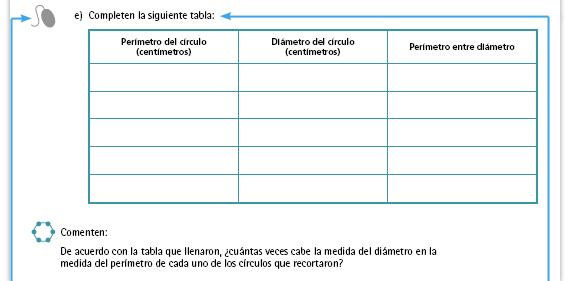
Propósito del interactivo. Mostrar que la relación entre el perímetro y el diámetro de un círculo es siempre igual al valor de , independientemente del tamaño del círculo.

Sugerencia didáctica. Se espera que al dividir el perímetro entre el diámetro los alumnos interpreten el cociente como el número de veces que cabe una medida en la otra; en este caso, el diámetro en el perímetro. Apoye a sus alumnos con preguntas como las siguientes: ¿Cuál es el dividendo? ¿Cuál es el divisor? ¿Qué representa el resultado de la división o cociente?

Sugerencia didáctica. Pida a los alumnos que copien esta información en el cuaderno, pueden ilustrarla pegando algunos de los círculos que recortaron y con los datos de la tabla anterior.

Propósito del video. Mostrar la obtención del número como el cociente de la división del perímetro de cualquier círculo entra la longitud de su diámetro.

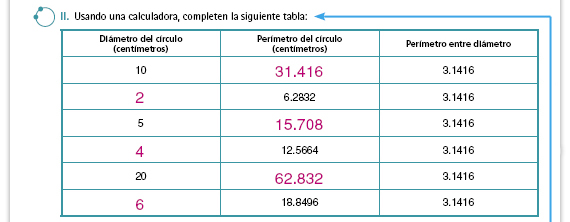
Propósito de la actividad. Se espera que los alumnos profundicen en la relación entre el diámetro y el perímetro: para conocer el perímetro se debe multiplicar 3.1416 por el diámetro, y dividir el perímetro entre 3.1416 para conocer el diámetro.

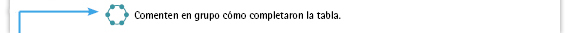
Sugerencia didáctica. Además de comparar los resultados, enfatice las relaciones entre el diámetro y el perímetro planteando las siguientes preguntas: Si conocemos el diámetro, ¿cómo obtenemos el perímetro? Si conocemos el perímetro, ¿cómo obtenemos el diámetro?

Propósito de la actividad. Que los alumnos identifiquen cómo varía el perímetro en función del diámetro, y que utilicen esa relación para resolver problemas; por ejemplo, si el diámetro disminuye a la mitad, el perímetro varía en la misma proporción.

Sugerencia didáctica. Si lo considera conveniente, antes de que los alumnos resuelvan los incisos b) y c), puede pedirles que hagan una estimación sobre cuántas vueltas tendría que dar la rueda delantera para recorrer 94 m. La finalidad de esa estimación es que se percaten de que la distancia es en metros, no en centímetros. Recomiéndeles que cada uno de ellos elija la unidad con la que quieren trabajar (metros o centímetros), para que antes de que empiecen a resolver, hagan las conversiones necesarias. Respuestas. b) 100 vueltas. c) 200 vueltas.