Propósitos de la sesión. Obtener una fórmula para calcular el perímetro del círculo. Resolver problemas de proporcionalidad que implican al número y a la fórmula del perímetro de un círculo. Organización del grupo. Se sugiere que la sesión se trabaje en parejas. Si lo considera conveniente, el apartado Lo que aprendimos puede resolverse de manera individual, o en parejas, como se indica. Materiales. Calculadora.

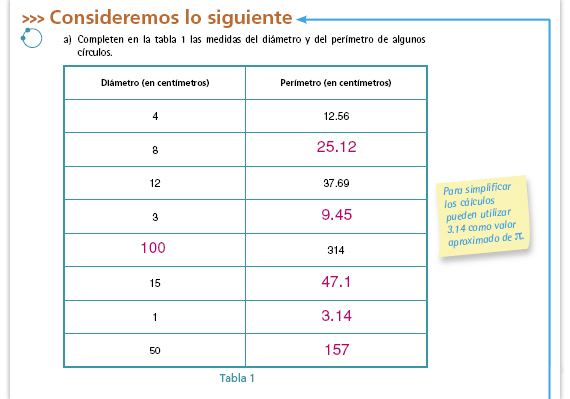
Posibles procedimientos. Se espera que los alumnos identifiquen la tabla 1 como una tabla de proporcionalidad y la resuelvan como tal, sin necesidad de utilizar la fórmula P = x d. No obstante, es posible que algunos alumnos apliquen directamente la fórmula, lo cual es correcto, sin atender las relaciones de proporcionalidad (por ejemplo, si el diámetro aumenta al doble o al triple, el perímetro aumenta en la misma proporción). También puede suceder que en los casos en los que la variación proporcional es evidente, se apoyen en algunas propiedades de la proporcionalidad (por ejemplo, al doble corresponde el doble), y que en otros apliquen la fórmula.

Respuestas. b) Aumenta el triple. Puede verse en la tabla con los diámetros de 4 y 12 y con los de 1 y 3. c) Disminuye a la mitad. Puede verse con los perímetros de 25.12 y 12.56, y con los de 314 y 157. d) La constante de proporcionalidad es . e) Perímetro = Diámetro x . Sugerencia didáctica. Tal vez algunos alumnos utilicen los números 3.14 o 3.1416 para expresar la fórmula para calcular el perímetro, sin embargo, lo correcto es que lleguen a la conclusión de que el perímetro es diámetro por y no diámetro por 3.14 o 3.1416. Es importante que en distintos momentos de la clase usted haga esa aclaración, para que no se queden con la idea de que la constante de proporcionalidad es la cantidad 3.1416 o 3.14. Lo correcto es que la constante de proporcionalidad es , y por eso el perímetro se calcula multiplicando el diámetro por (sin importar el valor aproximado que se tome de ).

Sugerencia didáctica. Reproduzca la tabla en el pizarrón para que algunas parejas pasen a poner sus respuestas. Aproveche el momento para enfatizar algunas de las propiedades de la proporcionalidad apoyándose en la tabla. Por ejemplo: si el diámetro aumenta al doble o al triple, ¿qué sucede con el perímetro?, ¿en qué casos a la suma de los diámetros le corresponde la suma de los perímetros?, ¿por cuánto debe multiplicarse cada una de las medidas del diámetro para obtener el perímetro que le corresponde?

Respuestas. a) El equipo 1 expresó la relación que hay entre el perímetro y el diámetro mediante una aproximación del valor de . El equipo 2 expresó una fórmula para encontrar el perímetro. Es importante subrayar con los alumnos que lo correcto es decir Perímetro = Diámetro por la constante de proporcionalidad, o bien, Perímetro = Diámetro por , y que como fórmula no es correcto decir Perímetro = Diámetro por 3.14 o 3.1416, dado que estas cantidades son aproximaciones de . b) La constante de proporcionalidad en la tabla 1 es (sin importar la aproximacion de su valor que se tome). c) Porque el equipo 1 utilizó la relación que hay del perímetro entre el diámetro y una de las aproximaciones del valor de , y el equipo 2 utilizó la fórmula para calcular el perímetro de un círculo.

Sugerencia didáctica. Comente con los alumnos esta información, enfatice que la constante de proporcionalidad es el número y no el valor aproximado de , el cual podría ser 3.14, 3.1416, 3.141598, o cualquier otra aproximación. Pida a los alumnos que copien esta información en el cuaderno y que den algunos ejemplos en los que se muestre como el diámetro y el perímetro del círculo varían proporcionalmente.

Pida a una pareja de alumnos que elabore un cartel con esta información, para que se cuelgue o se pegue en una de las paredes del salón de clases.

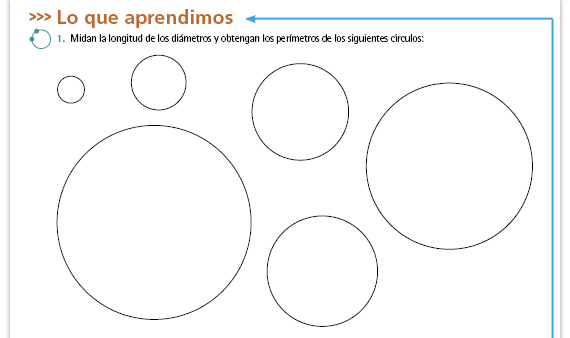
Posibles procedimientos. Los alumnos no necesitan realizar los cálculos en cada una de las circunferencias, bastará con que una vez obtenidas todas las medidas de los diámetros calculen el perímetro de una de ellas y, por medio de la proporcionalidad, obtengan las demás. Esto es posible porque los diámetros son proporcionales, miden 1, 2, 4, 6, 7 y 3.5 cm respectivamente. Si los alumnos se sienten inseguros con el uso de la proporcionalidad, pueden comprobar sus resultados haciendo las operaciones directas para cada circunferencia. Respuestas. La medidas aproximadas de los perímetros, son: 3.14, 6.28, 10.99, 12.56, 18.84 y 21.98 (de menor a mayor).

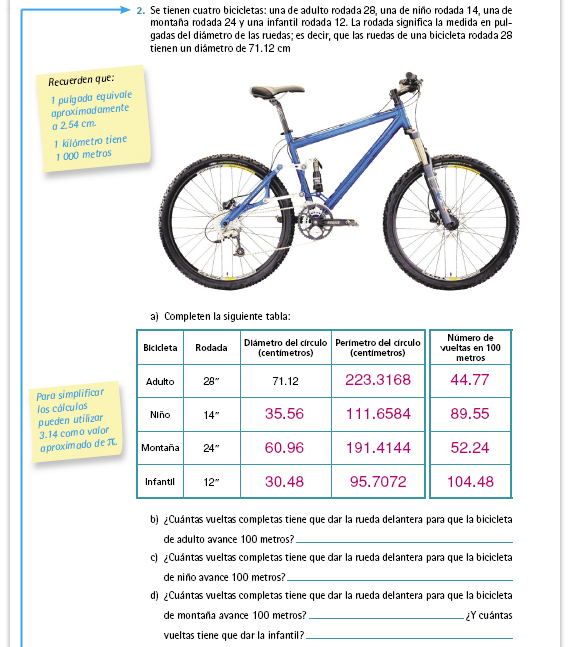
Integrar al portafolios. Igual que en el ejercicio anterior, es suficiente con que los alumnos obtengan el perímetro de 28" y 24", y a partir de ellos, el de 14" (es la mitad de 28") y el de 12" (es la mitad de 24"). Respuestas. -Para encontrar el diámetro se multiplica la rodada por 2.54. -Para encontrar el perímetro se multiplica el diámetro por 3.14. -Para encontrar el número de vueltas es necesario considerar que 100 m equivale a 10 000 cm, entonces hay que dividir 10 000 entre el perímetro. Para que sean vueltas completas, las cantidades pueden redondearse al entero siguiente: 45, 90, 53 y 105, respectivamente. Si los alumnos muestran dificultades en el cálculo de los perímetros, revise nuevamente con ellos el último apartado A lo que llegamos de esta sesión. Si nota que tienen dificultades para identificar la relación proporcional que existe entre las bicicletas de adulto y de niño, y entre las bicicletas de montaña y la infantil, haga preguntas similares a las que se le sugieren para el apartado Consideremos lo siguiente de esta sesión.

Respuestas. a) El primer nivel costará $1884.00. Este resultado se obtuvo de la siguiente manera: el perímetro es de 12.56 metros (tomando a como 3.14), se multiplica eso por el costo por metro y se obtiene el precio total del primer nivel. b) Se pueden pagar 5 niveles. Esto es, se divide 9 500 entre 1 884. c) Se pusieron 4 niveles. Esto es, se divide 7 539.84 entre 1 884. d) Costará $15 079.68. Esto es, se multiplica 7 539.84 por 2.