Propósito de la sesión. Identificar la fórmula del área de un círculo a través de la fórmula del área de un polígono regular y calcular algunas áreas. Organización del grupo. Se sugiere que trabajen en parejas durante toda la sesión. Materiales. Calculadora y regla.

Eje

Forma, espacio y medida.

Tema

Medida.

Antecedentes

En la escuela primaria los alumnos aproximaron áreas de círculos y de figuras curvas mediante el conteo de cuadrículas. En este grado de la educación secundaria los alumnos aprenderán a calcular el área del círculo mediante el uso de la fórmula. Para ello, se apoyarán en el cálculo de áreas de paralelogramos y de polígonos regulares que estudiaron en la secuencia 14.

Propósitos de la secuencia Resolver problemas que impliquen calcular el área y el perímetro del círculo.
Sesión	Título y propósitos de la sesión	Recursos
1	Área del círculo Identificar la fórmula del área de un círculo a través de la fórmula del área de un polígono regular y calcular algunas áreas.	Video "Área del círculo" Interactivo "Cálculo del área del círculo de Arquímedes" "Área del círculo" Aula de medios "Área del círculo" (Geometría dinámica)
2	Áreas y perímetros Resolver problemas que impliquen calcular el área y el perímetro del círculo.

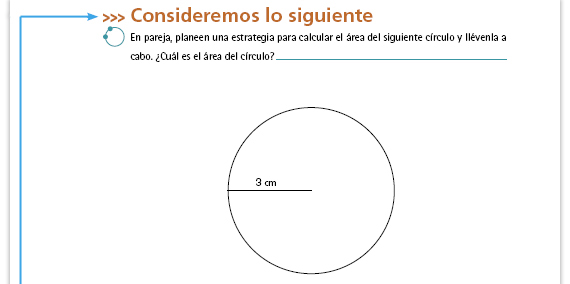
Posibles procedimientos. No se espera que los alumnos resuelvan correctamente el problema, sino que hagan uso de sus propios recursos para diseñar una estrategia que les permita aproximarse a la solución. Una posibilidad es que dividan el círculo en fi guras que ya conocen, por ejemplo, que lo dividan en varios triángulos iguales, que calculen el área de cada uno de ellos y después las sumen. De manera similar, pueden formar un polígono regular con un número de lados que ellos decidan, aunque entre mayor número de lados tenga el polígono, más se aproximará a la medida real del área del círculo. Si observa que tienen dificultades para establecer una estrategia de solución, usted puede sugerirles que dividan al círculo en figuras que ya conocen.

Sugerencia didáctica. Mientras las parejas resuelven, observe qué procedimientos utilizan para que en el momento de la comparación de resultados usted pueda elegir a dos o tres parejas que hayan empleado procedimientos distintos que se aproximen al área del círculo (por ejemplo, alguna que haya utilizado la triangulación, otra que haya trazado un pentágono y otra que haya trazado un polígono con un mayor número de lados). Pregunte al grupo qué procedimiento consideran que permite obtener un resultado más aproximado al área del círculo y por qué.

Propósito de las actividades. Ofrecer a los alumnos dos procedimientos que les permitan aproximarse al área del círculo haciendo uso de los conocimientos que ya tienen para calcular el área de paralelogramos y de polígonos regulares.

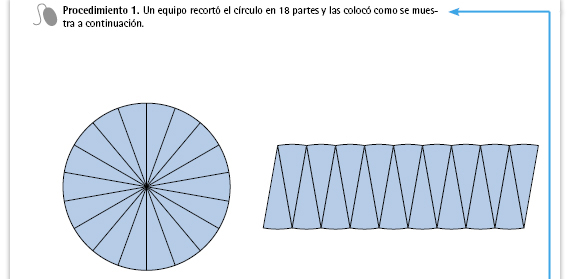
Propósito del interactivo. Mostrar una justificación de la fórmula para calcular el área del círculo.

Respuestas. a) Base × altura. (Si no lo recuerdan, los alumnos pueden repasar la secuencia 14). b) 3 cm aproximadamente. c) 9.4 cm aproximadamente. d) 28.3 cm2 aproximadamente. NOTA: Para los incisos c) y d) se utilizó = 3.14.

Propósito del interactivo. Mostrar dos procedimientos de aproximación al área de un círculo. Uno es numérico y el otro es simbólico.

Propósito de la actividad. Es importante que los alumnos concluyan que entre mayor sea el número de lados del polígono inscrito: a) Su área es más cercana al área del círculo. b) La apotema coincide con el radio del círculo. c) Por lo tanto, si sustituimos los datos en la fórmula del área de un polígono y se hacen algunas simplificaciones, tenemos que el área del círculo se puede calcular como si fuera un polígono regular: Área del círculo = x radio x radio.

Respuestas. a) El perímetro del polígono se acerca más al perímetro de la circunferencia. Haga notar a los alumnos que mientras más lados tenga el polígono su perímetro será mayor. b) La longitud del apotema se acerca más a la longitud del radio. También, mientras más lados tenga el polígono, su apotema será mayor. Recuerde a los alumnos que la apotema va del centro del polígono al punto medio de uno de los lados. c) d) por diámetro Es posible que no todos los alumnos puedan elaborar conclusiones a partir de las preguntas anteriores; no obstante, es importante que intenten establecer relaciones y elaborar argumentos. Si tienen dificultades no se preocupe, este procedimiento se detalla en el apartado A lo que llegamos. Una forma de establecer relaciones entre las preguntas anteriores, es la siguiente: -Cuando aumenta el número de lados del polígono, su área se parece más a la del círculo y la apotema se parece más al radio. El área del polígono es: El área del polígono es: -En el caso del círculo, el perímetro es igual a x diámetro, o 2 veces el radio, o 2 x radio. (Las tres formulas son equivalentes). -Entonces,

Sugerencia didáctica. Comente con los alumnos esta información y posteriormente pídales que vuelvan al problema inicial del apartado Consideremos lo siguiente y que verifiquen, aplicando la fórmula, el área del círculo.

Propósito del video. Mostrar la obtención de la fórmula del área del círculo mediante una aproximación por triangulaciones.

Respuestas. En cada caso se debe medir el radio. El área se obtiene con la fórmula: x r2.