Propósitos de la sesión. Solucionar problemas sencillos de conversión entre dos tipos de moneda para determinar e interpretar la expresión algebraica o relación funcional asociada al problema. Construir tablas para usar técnicas de proporcionalidad directa en la búsqueda de la expresión algebraica. Organización del grupo. Hay momentos de trabajo en grupo, de parejas e individual.

Eje

Manejo de la información.

Tema

Análisis de la información.

Antecedentes

En secuencias anteriores los alumnos han trabajado tanto situaciones de proporcionalidad directa como situaciones en las que deben expresar algebraicamente sucesiones numéricas, relaciones geométricas y entre cantidades que varían. En esta secuencia los alumnos estudiarán la representación algebraica de una variación específica: la proporcionalidad directa.

Propósitos de la secuencia Formular la expresión algebraica que corresponde a la relación entre dos cantidades que son directamente proporcionales. Asociar los significados de las variables en la expresión y = kx con las cantidades que intervienen en dicha relación.
Sesión	Propósitos de la sesión	Recursos
1	Cambio de moneda Solucionar problemas sencillos de conversión entre dos tipos de moneda para determinar e interpretar la expresión algebraica o relación funcional asociada al problema. Construir tablas para usar técnicas de proporcionalidad directa en la búsqueda de la expresión algebraica.	Video "Historia de la moneda" Interactivo "Variación proporcional 6"
2	Expresiones algebraicas y relaciones de proporcionalidad en distintos contextos Encontrar la expresión algebraica o la relación funcional cuando se aplican sucesivamente dos constantes de proporcionalidad. Una vez encontrada la expresión algebraica, hallar la inversa y notar las similitudes y diferencias entre estas dos expresiones algebraicas.

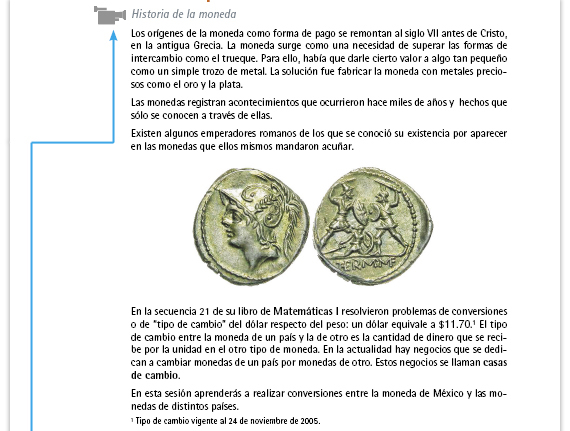
Propósito del video. Contextualizar a lo largo de la historia el problema del cambio de monedas mediante el establecimiento del "tipo de cambio".

Sugerencia didáctica. Comente a los alumnos que la peseta española fue la moneda oficial en ese país hasta 1999. Tras su incorporación a la Unión Europea la moneda oficial es el euro.

Posibles procedimientos. Los alumnos pueden utilizar distintas estrategias para hallar los valores que se les piden, por ejemplo, encontrar el valor unitario o hacer una tabla. Permítales utilizar cualquier procedimiento, incluso si es erróneo, más adelante tendrán oportunidad de verificar sus resultados. Respuestas a) Por un quetzal se reciben 1.40 pesos (se divide 210 entre 150), entonces por 8 quetzales se reciben 11.20 pesos (1.4 por 8). b) Por un dólar americano se reciben 11.70 pesos, por 13 dólares se reciben 152.10 pesos (11.7 por 13).

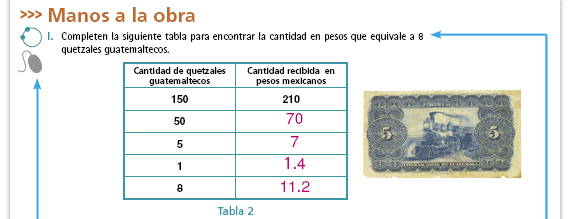
Propósito del interactivo. Deducir las expresiones algebraicas que corresponden a la relación entre dos cantidades que son directamente proporcionales.

Propósito de la actividad. En la sección Manos a la obra se privilegia el uso de la constante de proporcionalidad para la resolución del problema, ya que se pretende que el alumno asocie la ecuación de la forma y = kx a una situación de proporcionalidad directa. Respuestas. Es conveniente que escriban las cantidades con numeros decimales. Si algunos alumnos ponen indíqueles que lo escriban como 1.4. Sugerencia didáctica. Pregunte a los alumnos cuántos pesos y cuántos centavos son $1.4, porque es común que piensen que equivale a un peso con cuatro centavos. Explíqueles que un décimo de peso (0.1) es igual a la décima parte, es decir, a 10 centavos, por lo tanto, 0.4 son cuarenta centavos. Si lo prefieren, pueden escribir $1.40 para no confundirse.

Sugerencia didáctica. Comente con los alumnos esta afirmación y pregúnteles: -¿Qué significa que los quetzales guatemaltecos y los pesos sean cantidades directamente proporcionales? -¿Ocurrirá lo mismo entre el yen japonés y el peso? -¿Y entre el yen japonés y la libra esterlina? Sugerencia didáctica. Reconocer la constante de proporcionalidad es muy importante en esta secuencia para poder asociarle a la situación de cambio de moneda (y a otras que involucren relaciones de proporcionalidad directa) la expresión y = kx, por lo que vale la pena dedicarle un tiempo a esta pregunta si los alumnos tienen dificultades. Respuestas. La constante de proporcionalidad es 1.4 pesos por cada quetzal guatemalteco.

Sugerencia didáctica. Permita que se discuta en grupo la expresión algebraica. Para iniciar, puede ser útil plantear a los alumnos algunas preguntas como: ¿Cuál es la constante en la expresión? ¿Es una constante de proporcionalidad o aditiva? ¿Cuáles son las variables? ¿Qué significa 1.4x? ¿Alguien podría leer la expresión? ¿Alguien podría leer la expresión explicando el significado de las variables? (por ejemplo, "la cantidad de pesos y es igual a la cantidad de quetzales guatemaltecos x multiplicada por 1.4").

Sugerencia didáctica. Si sus estrategias anteriores fueron correctas deben obtener el mismo resultado al utilizar la expresión algebraica. Si hay resultados distintos, corríjanlos y averigüen cuál fue el error.

Sugerencia didáctica. Puede ser de utilidad que encuentren la constante de proporcionalidad que permite saber a cuántos pesos equivale cierta cantidad de dólares americanos. Esa constante es 11.7 pesos por cada dólar americano. Respuestas. Hay dos expresiones correctas (11.70x = y y y = 11.70x ). Si hay alumnos que tienen dificultad en reconocerlas puede pedirles que utilicen cada una de las seis expresiones para hallar la cantidad de pesos a los que equivalen , por ejemplo, 5 dólares (tendrían que obtener y = 58.5), para descartar aquellas que son erróneas. Sugerencia didáctica. Una vez que haya consenso sobre cuáles son las expresiones algebraicas correctas, escríbalas en el pizarrón y pida a los alumnos que las lean en voz alta y que expliquen en qué se parecen y en qué son diferentes. Como resultado de años de práctica con la aritmética, para muchos alumnos el signo igual ( = ) no significa que lo que está a la izquierda del signo sea equivalente a lo de su derecha, sino que lo de la derecha es el resultado de lo de la izquierda, es decir, el signo es unidireccional. Por eso es importante que se comenten casos como éste, en el que las expresiones son idénticas pero el término 11.70x aparece en uno u otro lado del signo igual.

Respuestas. Por una libra esterlina obtenemos 18.33 pesos (se divide 3 666 entre 200). Por una peseta obtenemos 0.0748 pesos (se divide 7.48 entre 100). Por un yen obtenemos 0.089 pesos (se divide 17.8 entre 200). Entonces las expresiones algebraicas son: Libra a peso y = 18.33x Peseta a peso y = 0.0748x Yen a peso y = 0.089x Sugerencia didáctica. Pida a los alumnos que a partir de las expresiones algebraicas digan: -Por cuál moneda extranjera (un dólar americano, un quetzal guatemalteco, etc.) dan más pesos al cambio. -Por cada peso, de cuál moneda extranjera puede comprarse una mayor cantidad.

Respuestas. a) Es 8.9 pesos por cada dólar canadiense. b) y = 8.9x y son los pesos x son los dólares canadienses. Sugerencia didáctica. Diga a los alumnos que investiguen las cotizaciones actualizadas de diversas monedas y realicen varios ejercicios de este tipo: encontrar la constante de proporcionalidad y la expresión algebraica que permiten realizar la conversión de una moneda a otra. Integrar al portafolios. Solicite a los alumnos una copia de sus respuestas a esta actividad y valore sus resultados. Si tienen dificultades, realicen más cambios entre monedas, averigüen cuál es la constante de proporcionalidad y escriban sus expresiones algebraicas.