
|

|

|
 |
 |

| Propósito de la sesión. Encontrar
la expresión algebraica o la relación
funcional cuando se aplican
sucesivamente dos constantes de
proporcionalidad.
Una vez encontrada la expresión algebraica, hallar la inversa y notar las similitudes y diferencias entre estas dos expresiones algebraicas. Organización del grupo. Se sugiere trabajar en parejas y de manera individual. |
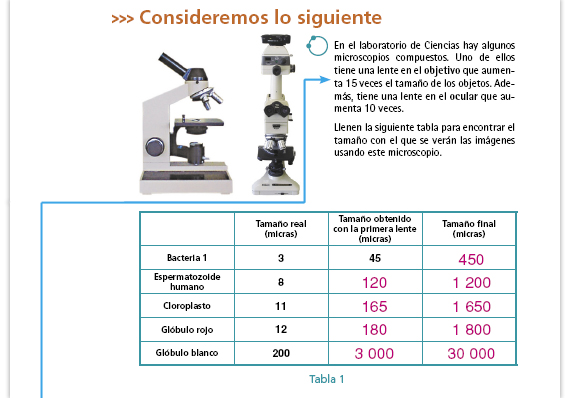
| Propósito de la actividad. Se espera que los alumnos puedan llenar la tabla con facilidad porque las han utilizado anteriormente en los temas de proporcionalidad. El desafío al que van a enfrentarse en esta actividad consiste en escribir expresiones algebraicas que den cuenta de las relaciones de proporcionalidad implicadas en la situación cuando se componen dos constantes de proporcionalidad. |

Respuestas.
|
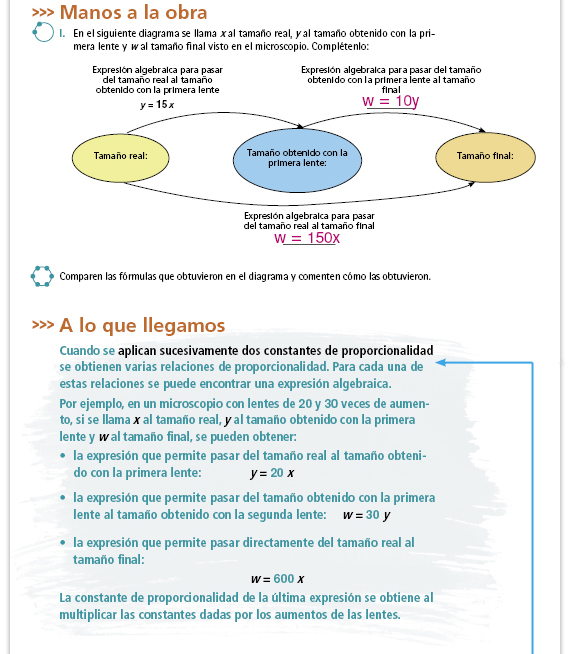
| Sugerencia didáctica. Proponga a los alumnos otros ejemplos de microscopios compuestos para que practiquen la escritura de expresiones algebraicas y pídales que averigüen cuál es la constante de proporcionalidad que les permite pasar del tamaño real al tamaño final. |

Respuestas.
Sugerencia didáctica. Recuerde a los alumnos que pueden utilizarse otras letras, siempre y cuando se indique el significado de cada una. Por ejemplo: d = 18l a = 18b m = 18n |
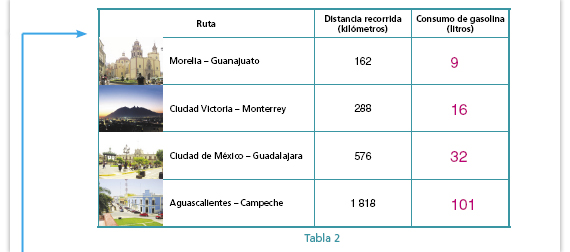
| Propósito de la actividad. Ahora los
alumnos tienen que averiguar cuál es
el consumo de gasolina conociendo la
distancia recorrida, o sea, se invierte
el lugar en el que se encuentra el
dato a hallar. En las tres preguntas
anteriores la situación era:
A tantos litros de gasolina  ¿Qué distancia recorre?
¿Qué distancia recorre?
Como se plantea en la tabla 2 es: A tantos kilómetros recorridos  ¿Cuántos litros de gasolina se consumen?
¿Cuántos litros de gasolina se consumen?
Ambos casos son parte de una misma relación de proporcionalidad directa, pero se invierte el conjunto de partida: en el primer caso es el consumo de gasolina y en el segundo la distancia recorrida. Para los alumnos esto implica encontrar dos constantes de proporcionalidad, una inversa de la otra: 18 km por litro y 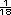 de litro por km. de litro por km.
|

Respuestas.
|
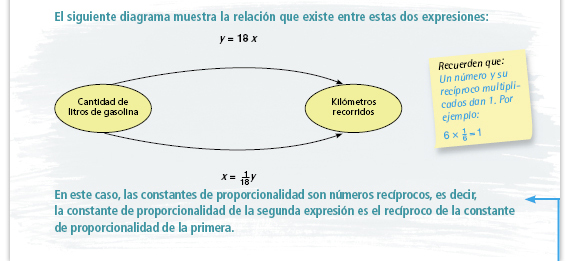
Sugerencia didáctica. Copie en el
pizarrón el diagrama y analícenlo
juntos. Pregunte a los alumnos:
|

| Integrar al portafolios. Guarde
una copia de las respuestas de cada
alumno a las preguntas de esta
sección. Si después de revisarlas
considera necesario hacer un repaso,
vuelvan a las secciones Manos a la
obra de esta secuencia.
Respuestas.
|
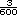 =
= 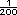 de
milímetro. Expresado como número
decimal es 0.005 milímetros o 5 micras
(una micra es 0.001 milímetros).
de
milímetro. Expresado como número
decimal es 0.005 milímetros o 5 micras
(una micra es 0.001 milímetros).
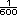 y (siguiendo la nomenclatura
anterior).
y (siguiendo la nomenclatura
anterior).