Propósito de la sesión. Resolver problemas que impliquen el cálculo de áreas de figuras formadas por rectas. Organización del grupo. Se sugiere que los alumnos resuelvan las actividades trabajando en parejas. Materiales. Regla.

Eje

Forma, espacio y medida.

Tema

Medida.

Antecedentes

En esta secuencia se espera que los alumnos apliquen lo aprendido en secuencias anteriores, particularmente las secuencias 20 y 30, para calcular el área de figuras formadas por rectas o por círculos, para las que no hay una fórmula inmediata, pero en las que se puede recurrir al cálculo de figuras conocidas.

Propósitos de la secuencia Resolver problemas que impliquen el cálculo de áreas de diversas figuras planas.
Sesión	Título y propósito de la sesión	Recursos
1	Áreas de figuras formadas por rectas Resolver problemas que impliquen el cálculo de áreas de figuras formadas por rectas.	Video "Geometría andaluza" Aula de medios "Áreas de figuras formadas por rectas" (Geometría dinámica)
2	Áreas de figuras formadas por círculos Resolver problemas que impliquen el cálculo de áreas de figuras formadas por círculos o semicírculos.	Aula de medios "Áreas de figuras formadas por círculos" (Geometría dinámica)

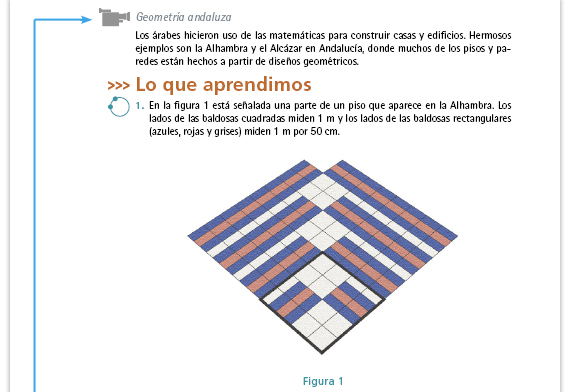
Propósito del video. Visualizar algunas de las creaciones artísticas árabes que han sido relevantes en la historia del pensamiento geométrico.

Respuestas. a) 16 m2. Este resultado puede obtenerse de distintas maneras: dos baldosas rectangulares equivalen a una cuadrada, entonces la medida de cada lado de la figura delimitada por la línea negra mide 4 m × 4 m = 16 m2. También pueden calcular el área de una baldosa rectangular y multiplicarla por el número de baldosas rectangulares (0.5 m2 × 16 = 8 m2), y luego sumar ese resultado con el área total de las baldosas cuadradas: 8 m2+ 8 m2 = 16 m2. b) 10 m2. Son 8 baldosas cuadradas y 4 baldosas rectangulares. Cada baldosa cuadrada tiene 1 m2 de superficie, y cada baldosa rectangular tiene 0.5 m2 de superficie. En total son 8 m2 + 2 m2= 10 m2. c) El área azul son 8 baldosas rectangulares, el área roja son 4 baldosas rectangulares. Es decir que el área azul es el doble de la roja.

Sugerencia didáctica. Los alumnos deben llegar a los mismos resultados, pero los procedimientos para resolver pueden ser distintos. Procure que se comparen al menos dos procedimientos diferentes.

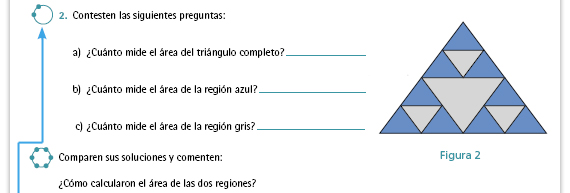
Respuestas. a) La base es de 6 cm, la altura es de 4 cm. El área del triángulo completo es de 12 cm2. b) 6.75 cm2. Hay distintas formas de llegar a este resultado. Una de ellas es calcular la medida de cada triángulo pequeño (los triángulos pequeños, azules y grises, miden lo mismo). Para ello puede tomarse como referencia el área del triángulo gris mayor, pues el triángulo completo puede dividirse en 4 triángulos iguales al triángulo gris mayor. El área de cada uno de ellos es: Cada uno de esos triángulos se divide a su vez en 4 triángulos pequeños iguales. El área de cada uno de ellos es de 0.75 cm2 (esto se obtiene dividiendo el área del triángulo gris mayor entre 4). El área de la región azul son los 9 triángulos azules pequeños; por lo tanto, el área de la región azul es 0.75 × 9 = 6.75 cm2. c) 5.25 cm2. Esto puede obtenerse de diversas formas: restando al área total el área azul; o bien, contando cuántos triángulos grises pequeños hay en total (el triángulo gris mayor equivale a 4 pequeños, en total son 7 triángulos grises pequeños), y multiplicando por 0.75.

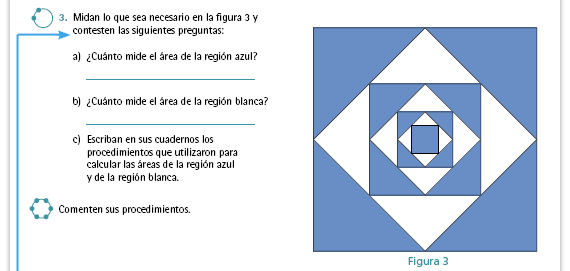
Posibles procedimientos. Hay distintas formas de resolver este problema. Una de ellas consiste en calcular el área de cada uno de los triángulos que forman las superfi cies blancas y azules. El área azul está formada por los cuatro triángulos azules grandes, cuatro azules medianos, cuatro azules pequeños y el cuadrado azul pequeño del centro. Cada triángulo azul grande tiene un área de 8 cm2, cada triángulo azul mediano tiene 2 cm2, cada triángulo azul pequeño tiene 0.5 cm2, y el cuadrado azul pequeño tiene un área de 1 cm2. La suma del área de los triángulos azules grandes es de 32 cm2, la de los medianos es de 8 cm2, y la de los pequeños es de 2 cm2. El área azul es: 32 cm2+ 8 cm2 + 2 cm2+ 1 cm2 = 43 cm2 Siguiendo el mismo procedimiento, el área blanca es: 16 cm2+ 4 cm2+ 1 cm2= 21 cm2 (Puede observarse que dentro de cada cuadrado hay otro cuadrado cuya área es la mitad del área del cuadrado que lo contiene). Otro procedimiento consiste en tomar como referencia al cuadrado pequeño que se ubica al centro de la figura. El área de este cuadrado es de 1 cm2. A partir de él se puede cuadricular toda la figura, de manera tal que es posible, mediante el conteo de unidades cuadradas de 1 cm2, obtener el área de la región azul y de la región blanca.