
|

|

|
 |
 |

| Propósito de la sesión. Resolver
problemas que impliquen el cálculo de
áreas de figuras formadas por círculos
o semicírculos.
Organización del grupo. Se sugiere que los alumnos resuelvan trabajando en parejas. Materiales. Regla y compás. |
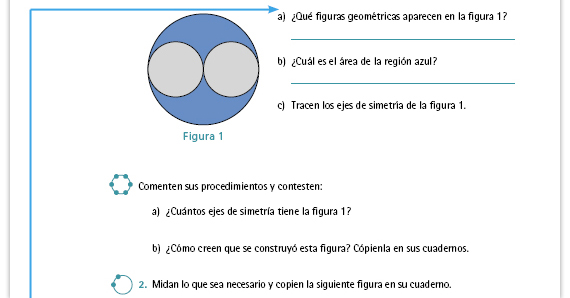
Respuestas.
|
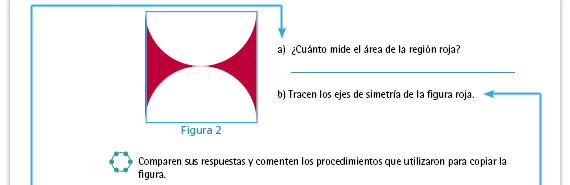
| Respuesta. El área de la región roja es de 3.44 cm2. Una manera de resolver es trazar un cuadrado como se muestra en la ilustración y obtener su área. El área del cuadrado (16 cm2) menos el área de los dos semicírculos. Los dos semicírculos juntos hacen un círculo con un diámetro de 4 cm, y el área de ese círculo es 12.56 cm2. La diferencia entre el área del cuadrado y el área del círculo es de 3.44 cm2. | Respuesta. Tiene dos ejes de simetría.
Una recta horizontal y una recta
vertical.
Recuerde que: La actividad de medir puede dar lugar a la obtencion de distintas medidas, por lo que es importante considerar aproximaciones y margenes de error aceptables. Particularmente cuando se trabaja con el área del círculo, lo que obtenemos son medidas aproximadas porque el valor que se toma para  es solo una
aproximación. es solo una
aproximación. |

| Respuesta. El área de la región roja es 1.935 cm2. Se obtiene calculando el área del cuadrado (9 cm2) y restándole el área de la región blanca. Esta última está formada por cuatro cuartos de círculo, que juntos forman un círculo con diámetro de 3 cm, cuya área es de 7.065 cm2. La diferencia entre el área del cuadrado y del círculo es de 1.935 cm2. |
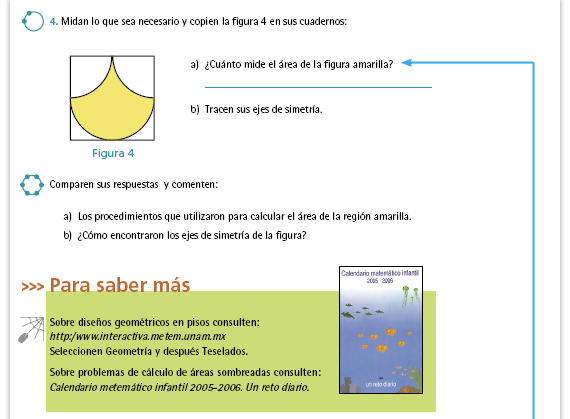
| Respuesta. El área amarilla mide 4.5 cm2. Esto puede obtenerse dividiendo el cuadrado en dos mitades con una línea horizontal que pase por el centro el cuadrado. El área amarilla de la mitad superior del cuadrado es la mitad del cuadrado menos medio círculo (el medio círculo se forma juntando los dos arcos): 4.5 - 3.5325 = 0.9675 cm2. El área amarilla de la mitad inferior del cuadrado es medio círculo: 3.5325 cm2. En total es: 0.9675 + 3.5325 = 4.5 cm2. |