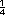|

|

|
 |
 |

| Propósitos de la sesión. Analizar la
diferencia entre un juego de azar justo y
uno injusto considerando la probabilidad
clásica.
Organización del grupo. El problema inicial debe resolverse en equipos, el resto de la sesión puede trabajarse en parejas. Materiales. Solicite a los alumnos con anticipación, que construyan una ruleta como la que se muestra en el dibujo. Pueden usar cartoncillo u otro material, lo importante es que la ruleta pueda girar. |
| Eje |
| Manejo de la información. |
| Tema |
| Nociones de probabilidad. |
| Antecedentes |
| En la secuencia 24 los alumnos tuvieron la oportunidad de enumerar los posibles resultados de una experiencia aleatoria, estudiaron cómo utilizar la escala de la probabilidad entre 0 y 1 y establecieron cuál de dos o más eventos en una experiencia aleatoria tiene mayor probabilidad de ocurrir. Esos conocimientos son necesarios en esta secuencia para poder establecer si un juego es equitativo o no de acuerdo con determinadas condiciones. |
| Propósitos de la secuencia
Reconocer las condiciones necesarias para que un juego de azar sea justo, con base en la noción de resultados equiprobables y no equiprobables. |
||
| Sesión | Título y propósitos de la sesión | Recursos |
| 1 | ¿Cuál es la mejor opción? Analizar la diferencia entre un juego de azar justo y uno injusto considerando la probabilidad clásica. | |
| 2 | Ruletas Reconocer las condiciones necesarias para que un juego de azar sea justo, con base en la noción de resultados equiprobables y no equiprobables. | Interactivo "La ruleta" |
| 3 | Juegos con dados Reconocer las condiciones necesarias para que un juego de azar sea justo a partir de las reglas que se dan en el juego. | |
| 4 | Quinielas Reconocer las condiciones necesarias para que un juego de azar sea justo a partir de los premios que se reparten. | Video
"Pronósticos nacionales" Interactivo "Lanza monedas" |
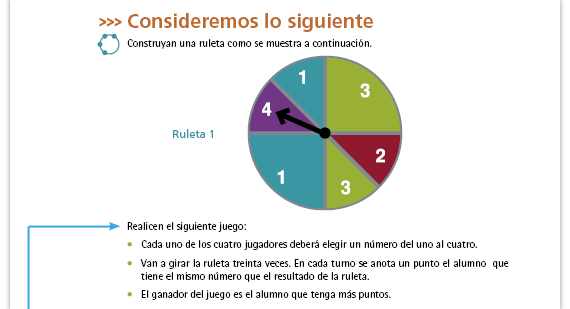
| Sugerencia didáctica. Asegúrese de que los alumnos tengan bien comprendidas las instrucciones; por ejemplo, si en el tercer turno cae 4, el alumno que fue numerado con 4 se anota un punto o una X en el casillero de la tabla que corresponde al turno 3. También se recomienda que usted enumere a los alumnos del 1 al 4 cuantas veces sea necesario, y luego les pida que formen equipos de cuatro; otra manera de formar los equipos es colocando papelitos en una bolsa con números del 1 al 4 y que cada alumno tome uno (en la bolsa deberá haber tantos papelitos como alumnos hay en el salón). |

| Sugerencia didáctica. Algunos podrían
decir que tienen más ventaja los números
1 y 3; pídales que expresen las razones de
por qué puede suceder eso y que realicen
el juego.
Respuesta. Los que tienen mayores posibilidades de ganar son el 1 y el 3, pues cada uno de ellos tiene  de probabilidad
en cada tiro. El 2 y el 4 tienen de probabilidad
en cada tiro. El 2 y el 4 tienen 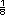 de
probabilidad cada uno. de
probabilidad cada uno. |

| Respuesta. Es muy probable que no se obtengan los mismos resultados. |
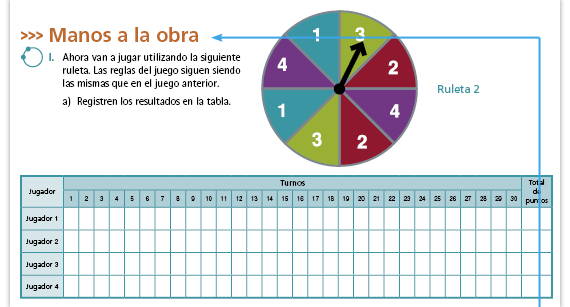
| Propósito de la actividad. En este caso, todos los sectores de la ruleta son iguales y los números aparecen dos veces cada uno; es decir, todos los jugadores tienen las mismas oportunidades de ganar. |

| Sugerencia didáctica. Si lo considera necesario, recuerde a los alumnos que la probabilidad frecuencial se basa en los resultados del juego: el número de veces que cayó el número ganador sobre el número de eventos. |

| Propósito de la actividad. En esta ruleta todos los sectores son del mismo tamaño y los números aparecen una sola vez cada uno; en ese sentido, esta ruleta es equivalente a la ruleta anterior porque todos los números tienen la misma posibilidad de ganar. Sin embargo, esto no significa que al realizar el juego el ganador sea el mismo de la ruleta anterior, ni tampoco que ya no podrá ganar. |
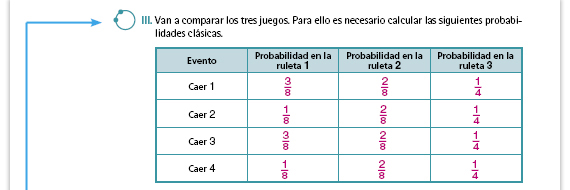
| Propósito de la actividad. Con esta tabla los alumnos podrán determinar si el juego con cada una de las ruletas es justo o no. Para ello, será necesario cálcular la probabilidad clásica de cada evento, para después poder compararlas. Algo importante que los alumnos deben comprender es que los resultados que obtuvieron al realizar los juegos no necesariamente reflejan si el juego es justo o no, sino que requieren hacer otros análisis de las condiciones del juego (en este caso comparar las características de cada ruleta y la probabilidad clásica de los eventos); cuando no se hacen estos análisis, las personas suelen atribuir a cuestiones de suerte el que ganen o pierdan en un juego. |

Respuestas.
|

 Pida a una pareja de alumnos
que elaboren un cartel con esta
información para que se pegue o se
cuelgue en una de las paredes del
salón. Para comentar esta información
puede indicarles que vean si se
cumplen estas condiciones en alguna
de las ruletas que revisaron en
esta sesión. Posteriormente pídales
que copien la información en sus
cuadernos. Pida a una pareja de alumnos
que elaboren un cartel con esta
información para que se pegue o se
cuelgue en una de las paredes del
salón. Para comentar esta información
puede indicarles que vean si se
cumplen estas condiciones en alguna
de las ruletas que revisaron en
esta sesión. Posteriormente pídales
que copien la información en sus
cuadernos. |
 es equivalente a
es equivalente a