
|

|

|
 |
 |

| Propósito de la sesión. Reconocer
las condiciones necesarias para que un
juego de azar sea justo, a partir de las
reglas que se dan en el juego.
Organización del grupo. Se sugiere que los alumnos trabajen en parejas. Materiales. Solicite a los alumnos que elaboren con anticipación los dados que se describen en el apartado Consideremos lo siguiente. |
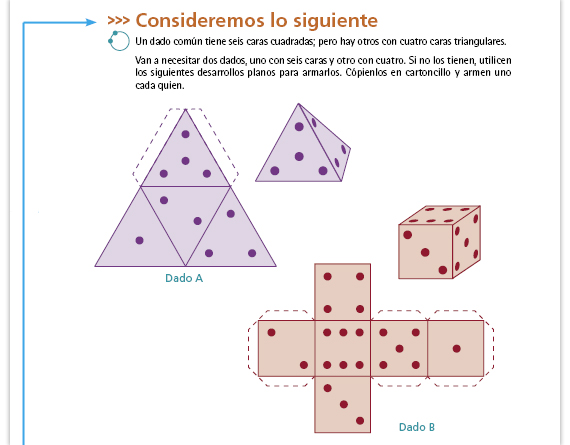
| Propósito de la actividad. Que los alumnos experimenten con diferentes objetos qué condiciones se deben dar para que un juego sea justo; en este caso, se trata de un juego con dados de diferente forma. |

Respuesta.
En el dado 1 la probabilidad clásica de obtener el 3
es 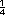 . En el dado 2 es . En el dado 2 es 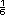 .
Es más
probable que salga primero un 3 en el
dado 1. .
Es más
probable que salga primero un 3 en el
dado 1. |

Respuesta.
Es la misma probabilidad.
En el dado 1 la probabilidad clásica de
obtener un número impar es 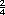 , en el
dado 2 es , en el
dado 2 es 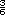 . Son equivalentes. . Son equivalentes. |

| Sugerencia didáctica. Es importante que los alumnos lleven el registro del número de lanzamientos, pues este dato les será necesario para responder el inciso b). |

Respuestas.
|

| Propósito de la actividad. En esta
actividad lo que están cambiando es el
evento a partir del cual se obtienen los
resultados, a diferencia de la sesión
anterior, donde cambiaban las ruletas
pero el evento (caer 1) se mantenía.
Es importante determinar los espacios
muestrales (es decir, todos los
resultados posibles) y calcular la
probabilidad en cada dado del evento.
Sugerencia didáctica. Es importante que los alumnos lleven el registro del número de lanzamientos, pues este dato les serán necesario para responder el inciso b). |

Respuestas.
|

| Propósito de la información. En las siguientes actividades se le llama "regla" al evento que se considera para determinar las condiciones para realizar el juego. En cada dado varía la probabilidad de que ocurra cada una de las reglas . |

| Posibles respuestas. Cae un número menor que 5. Cae algún número entre 1 y 4. El número es mayor que 0 y menor que 5. Cae un número con una cifra. Cae un número menor que 10. |

| Sugerencia didáctica. Se espera que la respuesta sea afirmativa, pero en caso de que no sea así, invite a los alumnos a que revisen nuevamente los eventos que escribieron. |

| Posibles respuestas.
Cae un número par.
Cae un número impar. Cae 10 (nunca se avanza). |