
|

|

|
 |
 |

| Propósitos de la sesión. Reconocer
las condiciones necesarias para que un
juego de azar sea justo, a partir de los
premios que se reparten.
Organización del grupo. Se sugiere que el problema inicial y la primera actividad del Manos a la obra se resuelva en equipos, y posteriormente que trabajen en parejas. |

| Propósito del video. Conocer qué es y cómo se llena una quiniela. Identificar las posibilidades que se tienen de ganar al jugar una quiniela. |
| Sugerencia didáctica: Pida a los alumnos que lean el ejemplo que se muestra de una quiniela. Pregunte quiénes han llenado alguna vez una de ellas; pida a esos alumnos que expliquen a los demás qué quieren decir los términos "local", "visitante", "empate", y que comenten cómo se llena la quiniela. Aproveche este momento para que los alumnos intercambien con el grupo lo que saben al respecto. |
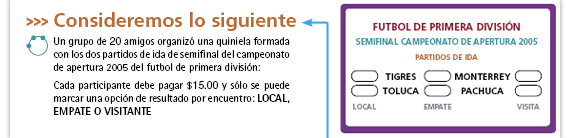
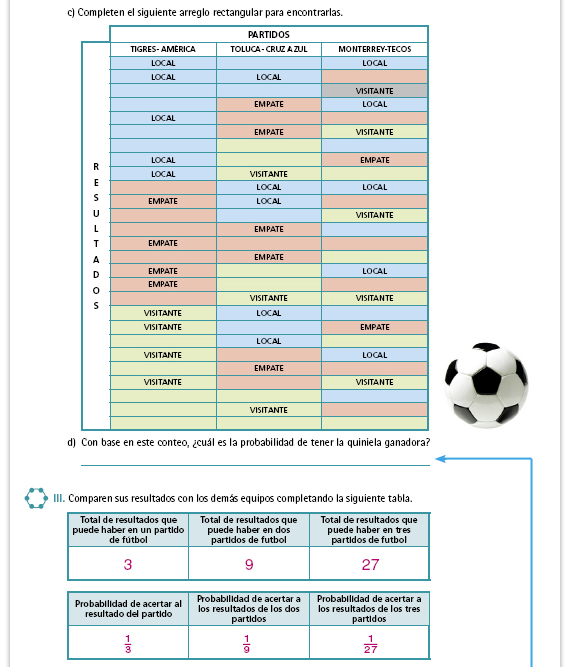
| Propósito de la actividad. Tal vez algunos alumnos han visto o llenado una quiniela; con esta actividad se espera que analicen algunos factores que pueden influir en el resultado de la misma. Para ello, se idealizan ciertas condiciones para que el análisis pueda hacerse a partir de la cantidad de resultados que se pueden dar. |
Respuesta.
La probabilidad de
acertar es de 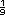 . Es probable que
algunos piensen que es de . Es probable que
algunos piensen que es de 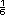 , porque
son 3 posibilidades por partido.
Si contestaron erróneamente, en
el siguiente apartado tendrán
oportunidad de corregirlo. , porque
son 3 posibilidades por partido.
Si contestaron erróneamente, en
el siguiente apartado tendrán
oportunidad de corregirlo. |

Respuestas.
|
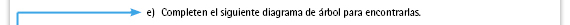
| Propósito de la actividad. El diagrama de árbol o cualquier otro recurso que utilicen para contar les servirá de apoyo para encontrar los resultados. |
Respuesta.
La probabilidad es 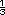 ; si hay 2 partidos, la
probabilidad es ; si hay 2 partidos, la
probabilidad es 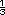 x x 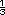 =
= 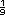 . .
Es decir, se multiplica la probabilidad de cada partido porque son resultados independientes. |
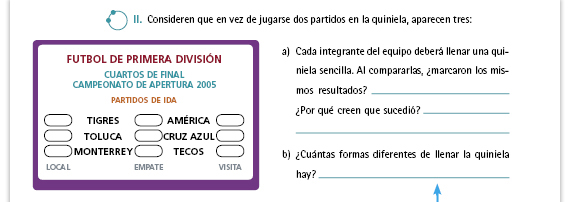
| Respuestas. Hay 27 formas diferentes de llenarla. Se calcula 3 × 3 × 3. |
Respuesta. Es de
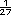 |

Respuestas.
Sugerencia didáctica. Pregunte cuál es la probabilidad de acertar en una quiniela con 14 partidos, como las que se utilizan en los pronósticos.
|

Respuestas.
|

| Respuestas. No es justa, porque es menos probable obtener el primer lugar. |

| Sugerencia didáctica. Es posible que sea mejor iniciar revisando las propuestas de la tabla en el inciso d), luego puede pedirles que hagan nuevas propuestas. |

| Respuesta.
(Una forma de entenderlo es que el
primer lugar es el que acierta a los 3
resultados. El segundo lugar es el que
acierta a 2 resultados).
El primer lugar tiene 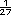 de
probabilidad.
El segundo lugar tiene de
probabilidad.
El segundo lugar tiene 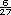 de
probabilidad.
Es decir que obtener el primer lugar
es 6 veces menos probable que
obtener el segundo lugar.
Lo justo es que el primer lugar reciba
6 veces mas de premio. Con $300
pesos deben repartirse asi:
$257.14 al primer lugar.
$42.86 al segundo lugar. de
probabilidad.
Es decir que obtener el primer lugar
es 6 veces menos probable que
obtener el segundo lugar.
Lo justo es que el primer lugar reciba
6 veces mas de premio. Con $300
pesos deben repartirse asi:
$257.14 al primer lugar.
$42.86 al segundo lugar.
Sugerencia didáctica. Quizá esto sea complicado. Es mejor que usted permita que los alumnos decidan. Lo importante es que el primer lugar debe recibir más dinero que el segundo lugar. |
| Respuestas. Son 4 posibles resultados
en total. Los dos que se presentan:
Águila-Águila. Águila-Sol. Y dos más: Sol-Águila. Sol-Sol. |

| Propósito del interactivo. Desarrollar la intuición sobre los posibles resultados de lanzar una moneda en relación con el número de veces que se realicen los lanzamientos. |

| Integrar al portafolios. Pida a los alumnos que calculen la probabilidad de atinarle a una quiniela con cuatro partidos y que digan cuántas combinaciones habría. |
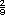 .
.