
|

|

|
 |
 |

| Propósito de la sesión.
Relacionar una expresión
algebraica a situaciones de proporcionalidad directa y
construir tablas y gráficas a partir de dichas situaciones.
Organización del grupo. A lo largo de la sesión hay momentos de trabajo grupal, en parejas e individual. |
| Eje |
| Manejo de la información. |
| Tema |
| Análisis de la información. |
| Antecedentes |
| En secuencias anteriores los alumnos han trabajado con situaciones directamente proporcionales, su representación en tablas y gráficas, y la escritura de su expresión algebraica. En esta secuencia se pretende que los alumnos reconozcan situaciones de proporcionalidad directa asociándolas con una tabla, gráfica y expresión algebraica correspondientes, y que encuentren valores faltantes a partir de cualquiera de sus representaciones. |
| Propósitos de la secuencia | ||
| Sesión | Título y propósitos de la sesión | Recursos |
| 1 | Gráficas, tablas y expresiones algebraicas asociadas a problemas de proporcionalidad directa Relacionar una expresión algebraica a situaciones de proporcionalidad directa y construir tablas y gráficas a partir de dichas situaciones. | Video "Elementos de la proporcionalidad directa" Aula de medios "Gráficas, tablas y expresiones algebraicas asociadas a problemas de proporcionalidad directa" (Hoja de cálculo) |
| 2 | De la gráfica al problema Relacionar una gráfica a situaciones de proporcionalidad directa y escribir la expresión algebraica correspondiente. | |

| Propósito del video.
Reconocer las características de
las representaciones tabular, gráfica y algebraica de
una situación de proporcionalidad directa.
Propósito de la actividad. Se pretende que los alumnos reconozcan una situación de proporcionalidad directa y la relacionen con una expresión algebraica. También se busca que observen que una misma expresión algebraica puede asociarse a varias situaciones. Sugerencia didáctica. Si los alumnos no están seguros de cuáles situaciones pueden asociarse a la expresión, sugiérales que prueben con distintos valores para x y vean si se cumple. Si eligen situaciones a las que es incorrecto asociarles la expresión, no los corrija y permítales avanzar en la resolución de la sesión. |

| Respuestas.
En la situación a) interesa averiguar
cuántos pesos se obtienen por cierta cantidad de
francos. Si y es la cantidad de pesos que se obtendrán
al hacer el cambio, x la cantidad de francos que van a
cambiarse y se sabe que por cada franco se obtienen
dos pesos, entonces la situación sí tiene asociada la
expresión y = 2x
.
En la situación b) se sabe que cuando Luis tenga 16 años será el doble de la edad de Laura, pero para cualquier otra edad de Luis esa diferencia ya no será del doble, así que no puede asociársele la expresión porque la situación no es de proporcionalidad directa. En la situación c) se quiere averiguar el costo de cierto número de llamadas (y), cada llamada (x ) cuesta dos pesos, por lo tanto, sí se le puede asociar la expresión y = 2x. En la situación d) interesa conocer cuántos pesos mexicanos (y) se obtienen por cierta cantidad de pesos uruguayos (x), y como por cada peso uruguayo se obtienen 50 centavos de peso mexicano, la expresión no es correcta. La que corresponderia es y = 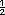 x. Si la
situación fuera a la inversa, es decir, hallar cuántos
pesos uruguayos se obtienen al cambiar pesos
mexicanos, la expresión sí correspondería. x. Si la
situación fuera a la inversa, es decir, hallar cuántos
pesos uruguayos se obtienen al cambiar pesos
mexicanos, la expresión sí correspondería. |

| Sugerencia didáctica.
Los alumnos
ya estudiaron el concepto de
dependencia en la secuencia 27.
Pregúnteles qué variable está en
función de la otra en esta situación.
Respuestas. La expresión es y = 2x. |

| Respuestas.
La expresión es
v = u + 8, pero también podría ser u = v - 8 porque en esta situación no se especifica qué variable está en función de la otra. |


| Sugerencia didáctica. Dé un espacio para discutir grupalmente cuál de las tablas es de proporcionalidad directa. Pida a los alumnos que argumenten su respuesta. |
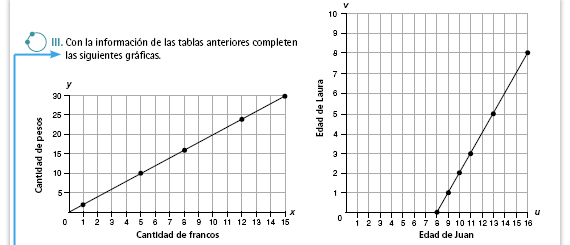
| Posibles dificultades. Cuando terminen de hacer las gráficas notarán que ambas son rectas, lo que puede hacer pensar a algunos alumnos que ambas situaciones son de proporcionalidad directa. Si esto ocurre, pídales que revisen la sección A lo que llegamos de la secuencia 32, sesión 2, en donde se explicita cómo deben ser las gráficas que representan una situación de proporcionalidad directa (en una recta que pasa por el origen -el punto 0, 0-, condición que la gráfica de las edades no cumple). |

| Sugerencia didáctica. Es
conveniente que se discuta el inciso
d). Si es una situación de
proporcionalidad directa, pero como
se dijo antes, no corresponde a la
expresión algebraica y = 2
x.
La expresión correcta para esa
situación sería
y = 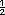 x. x.
Propósito de la actividad. Se pide a los alumnos hacer la tabla y la gráfica con la intención de que tengan más elementos para elegir cuál situación es de proporcionalidad directa y tiene asociada la expresión dada, o bien, para validar su respuesta cuando ya han hecho una elección. Una vez que terminen, regresen a la sección Consideremos lo siguiente y si hubo errores corríjanlos. |

|
Integrar al portafolios. Conserve
una copia de las respuestas de
los alumnos a esta actividad. Si lo
considera necesario, pídales que
justifiquen su respuesta haciendo
una tabla y/o gráfica para mostrar
que la situación que eligieron es
de proporcionalidad directa y que
corresponde a la expresión dada.
Respuestas. En la situación a) la ganancia ( y ) es de tres pesos por cada dos pesos invertidos ( x ). Sí es de proporcionalidad directa, pero no corresponde a la expresión dada. La expresión correcta sería y = 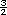 x.
Encontrar tal expresión puede ser
difícil para los alumnos, lo importante
es que reconozcan que la situación no
corresponde a la expresión dada.
En la situación b) la velocidad de
un automóvil ( y ) es el triple de la
velocidad de otro automóvil ( x ), por
lo tanto sí es correcto asociarle la
expresion y =
3x. x.
Encontrar tal expresión puede ser
difícil para los alumnos, lo importante
es que reconozcan que la situación no
corresponde a la expresión dada.
En la situación b) la velocidad de
un automóvil ( y ) es el triple de la
velocidad de otro automóvil ( x ), por
lo tanto sí es correcto asociarle la
expresion y =
3x.
En la situación c) la producción de la máquina ( y ) esta dada por el tiempo ( x ) que tarda en hacer una lata. Si en un segundo produce 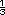 de lata, la
expresión correcta sería y = de lata, la
expresión correcta sería y =
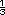 x.
Es una situacion de proporcionalidad
directa, pero no le corresponde la
expresion dada. x.
Es una situacion de proporcionalidad
directa, pero no le corresponde la
expresion dada. |