Propósito de la sesión. Construir y analizar tablas para determinar valores faltantes en una situación de proporcionalidad inversa. Organización del grupo. La sesión se resuelve en parejas, excepto la última sección, que es individual.

Eje

Manejo de la información.

Tema

Análisis de la información.

Antecedentes

Los alumnos han tenido contacto principalmente con situaciones de variación proporcional directa, sus propiedades y sus representaciones. En esta secuencia conocerán otro tipo de variación: la proporcionalidad inversa. También elaborarán tablas y gráficas para conocer valores faltantes y conocerán algunas de sus propiedades.

Propósitos de la secuencia Identificar y resolver situaciones de proporcionalidad inversa mediante diversos procedimientos.
Sesión	Propósitos de la sesión	Recursos
1	El agua Construir y analizar tablas para determinar valores faltantes en una situación de proporcionalidad inversa.
2	La velocidad Asociar la expresión algebraica correspondiente a problemas de cantidades inversamente proporcionales.	Video "La velocidad constante" Interactivo "Variación proporcional inversa y gráficas 1"
3	La hipérbola Asociar la expresión algebraica correspondiente a problemas de cantidades inversamente proporcionales y construir la gráfica correspondiente.	Interactivo "Variación proporcional inversa y gráficas 2" Aula de medios "La hipérbola" (Hoja de cálculo)

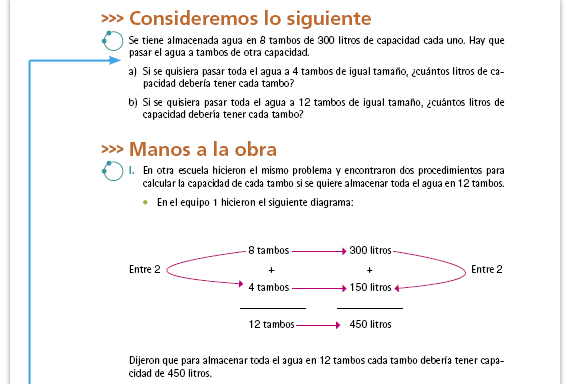
Propósito de la actividad. Los alumnos van a explorar situaciones de proporcionalidad inversa y formas correctas e incorrectas de resolver los problemas que se plantean. Posibles dificultades. Es común que los alumnos traten de resolver situaciones de proporcionalidad inversa utilizando procedimientos que han aprendido para la proporcionalidad directa, más aún porque su experiencia con la proporcionalidad inversa es mucho menor que la que han adquirido con la directa. Si los alumnos no reconocen la diferencia entre las situaciones planteadas en esta secuencia y las de proporcionalidad directa, no trate de explicárselas en este momento. En la sección Manos a la obra se presentan procedimientos de resolución incorrectos para que puedan analizarlos juntos y conocer las propiedades de la proporcionalidad inversa. Respuestas. a) El total de agua son 2 400 litros, si se reparte en 4 tambos cada uno debe tener una capacidad de 600 litros. b) Los 2 400 litros se reparten en 12 tambos, cada uno debe tener una capacidad de 200 litros.

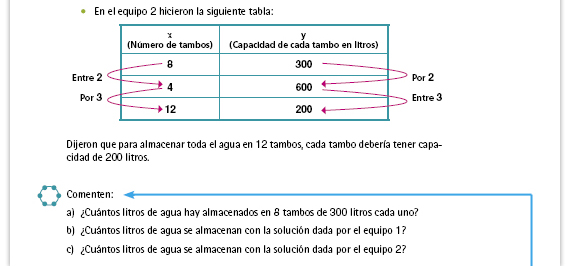
Respuestas. a) 2 400 litros. b) Son 12 tambos, cada uno con una capacidad de 450 litros, así que en total se almacenan 5 400 litros. c) Si cada uno de los 12 tambos tiene una capacidad de 200 litros, en total se almacenan 2 400 litros.

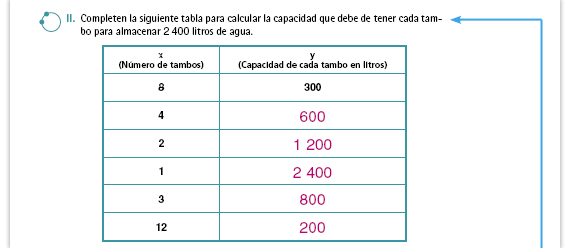
Sugerencia didáctica. Analicen la tabla cuando terminen de llenarla. Pregunte a los alumnos qué diferencias o similitudes encuentran en esta tabla con respecto a las de variación proporcional directa. Si ningún alumno lo comenta, dígales que observen que mientras mayor es el número de la columna izquierda (número de tambos), menor es el de la derecha (capacidad de cada tambo).

Respuestas. a) 240 litros. b) 2 400 litros. c) 75 litros.

Respuestas. a) Se multiplica por 2 el número de tambos. b) Se divide entre 5 el número de tambos. c) Si el número de tambos aumenta al doble, la capacidad se divide entre dos. Si el número de tambos disminuye la cuarta parte, la capacidad se multiplica por 4. Sugerencia didáctica. Revisen las respuestas a las preguntas de la sección Consideremos lo siguiente y corrijan si es necesario.

Sugerencia didáctica. Comenten esta información. Haga énfasis en que los procedimientos que aprendieron para resolver problemas en situaciones de proporcionalidad directa no les serán útiles cuando se trate de situaciones de proporcionalidad inversa. Puede poner algún ejemplo para aclararlo.

Integrar al portafolios. Revise las respuestas de los alumnos a esta actividad. Si fuera necesario, pídales que hagan una tabla para averiguar las respuestas. Respuestas. a) Con 60 pasajeros cada uno paga $30. b) $90 c) $120 d) El número de alumnos que va a la excursión y la cantidad que paga cada uno.