Propósito de la sesión. Asociar la expresión algebraica correspondiente a problemas de cantidades inversamente proporcionales. Organización del grupo. En la sesión se sugieren momentos de trabajo individual, en parejas y grupal.

Propósito del video. Ejemplificar la noción de velocidad constante.

Sugerencia didáctica. Antes de empezar a responder, pregunte a los alumnos cuál es la distancia que hay entre la Ciudad de México y la de Veracruz. Si el viaje dura 6 horas a una velocidad promedio de 70 km por hora, hay una distancia de 420 km. Respuestas. a) 35 km/h b) 140 km/h c) 84 km/h

Propósito del interactivo. Resolver problemas que involucran cantidades inversamente proporcionales, relacionando tablas, gráficas y su expresión algebraica.

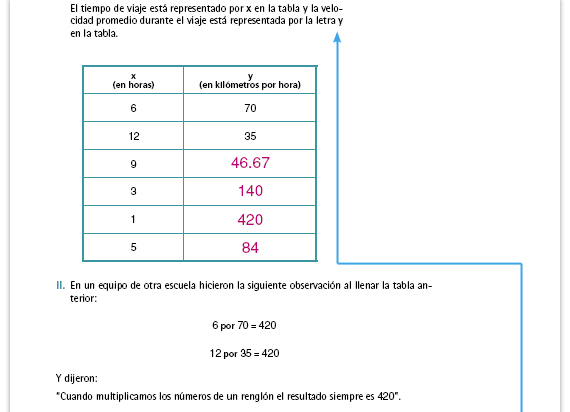
Sugerencia didáctica. Si los alumnos tienen dificultades para llenar la tabla, ayúdelos a encontrar las relaciones entre los datos. Por ejemplo, Horas km/h 6 70 12 35 la cantidad de horas del segundo renglón (12) es el doble que la del primero (6), y los kilómetros por hora del segundo renglón (35) son la mitad de los del primero (70). Esto tiene sentido, porque si se viaja a la mitad de velocidad, el recorrido durará el doble de tiempo. Ahora, para hallar los valores faltantes puede sugerirles que empiecen con el 3 (horas), ya que es la mitad del 6 y por lo tanto la velocidad será el doble. Conociendo ese dato pueden averiguar la velocidad a la que hay que viajar si el recorrido se hace en 9 horas (la velocidad será tres veces menor que si sólo dura 3 horas). Un viaje de 5 horas será cinco veces más lento que uno de una hora.

Respuestas. El resultado siempre es 420, que es la distancia entre la ciudad de Veracruz y la de México. Recuerde que. En una situación de proporcionalidad inversa: -cuando una cantidad aumenta el doble, la otra disminuye a la mitad, si aumenta el triple la otra disminuye a la tercera parte, etc.; -si se representa en una gráfica se obtiene una curva llamada hipérbola; -si se representan los datos en una tabla el producto entre los elementos de los dos conjuntos se mantiene constante; -su expresión algebraica es En una situación de proporcionalidad directa: -cuando una cantidad aumenta el doble, la otra también aumenta el doble, si aumenta el triple la otra también aumenta el triple, etc.; -si se representa en una gráfica se obtiene una recta que pasa por el origen; -si se representan los datos en una tabla el cociente entre los elementos de los dos conjuntos se mantiene constante; -su expresión algebraica es y = kx Sugerencia didáctica. Busquen una secuencia de proporcionalidad directa en la que hayan llenado una tabla. Pídales que multipliquen los números de cada renglón y vean si se obtiene un producto constante.

Respuestas. a) 420 km b) Por 84. Pueden pensarlo como 5x ___ = 420, o bien, 420 ÷ 5 = ___ c) Por 46.67 (redondeando).

Respuestas. No hay.

Respuestas. Se divide la constante de proporcionalidad inversa entre el otro dato conocido, en este caso, el tiempo. Entonces y =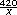

Respuestas. a) 210 km/h b) 60 km/h

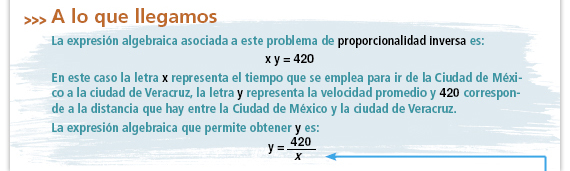
Sugerencia didáctica. Comparen esta expresión (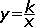) con y = kx, que es la que corresponde a las situaciones de proporcionalidad directa. Puede preguntar a los alumnos en qué se parecen y en qué se diferencian. Por ejemplo, qué papel juega la constante en cada uno de los casos (en la proporcionalidad directa la constante es el número por el cual se multiplica el dato de la primera columna para obtener el de la segunda; en cambio, la constante de proporcionalidad inversa es el número que resulta de multiplicar los datos de un mismo renglón).

Integrar al portafolios. Pida una copia de las respuestas de los alumnos al número I. Respuestas. La constante de proporcionalidad inversa es el número de litros que hay que almacenar, 2 400. La expresión sería y=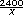

Posibles procedimientos. Los alumnos podrían fijarse en las relaciones que hay entre los datos: Campesinos Días 2 3 6 6 Si el número de campesinos aumenta de 2 a 6 (o sea, por 3), el número de días será una tercera parte del primero. Si el número de días en los que se termina el trabajo aumenta el doble (de 3 a 6), el número de campesinos que trabajarían sería la mitad. O bien, hallar la constante de proporcionalidad inversa, que corresponde a 6 días de trabajo total (ya saben que si se multiplican los datos de un renglón se obtiene esa constante). Respuestas a) Un día. b) Un campesino.