Propósito de la sesión. Asociar la expresión algebraica correspondiente a problemas de cantidades inversamente proporcionales y construir la gráfica correspondiente. Organización del grupo. Todas las actividades son en parejas, salvo la última, que es individual.

Propósito de la actividad. Ahora la proporcionalidad inversa se aborda en la geometría, dejando como constante el área y variando la longitud de los lados. Respuestas. a) 4 cm porque 6 × 2 = 24. b) 2 cm porque 12 × 2 = 24. c) 3 cm porque 8 × 3 = 24. d) La base y la altura del rectángulo. e) 24 porque es el número que se obtiene siempre que se multiplica la base por la altura. f) Si la base es x y la altura y, entonces yx = 24 o y = Posibles dificultades. Para muchos alumnos las expresiones yx = 24 y y = 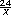son dos cosas independientes que se aprenden por separado. Es importante hacerles ver que estan relacionadas y que la forma de "acomodarlas" depende de cual sea el valor que debe hallarse y cuáles ya se conozcan. En este ejemplo, si quiere hallarse la constante de proporcionalidad inversa la expresión sería xy = k Si ya se conocen la base y la constante, entonces y = 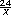. Y si hay que averiguar cuál es la base conociendo la constante y la altura x = 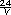. Pero los alumnos no tienen que aprenderse una por una, el objetivo es que conociendo la expresión algebraica de la proporcionalidad inversa puedan hallar cualquier valor. Para lograrlo puede ser útil analizar la expresión y utilizarla varias veces en diferentes situaciones, dándole distintos valores a una de las variables y manteniendo la constante. Después hacer lo mismo con la otra variable y analizar los cambios.

Propósito del interactivo. Ejemplificar la noción de velocidad constante.

Sugerencia didáctica. Cuando terminen de llenar la tabla verifiquen que efectivamente xy = 24.

Sugerencia didáctica. Si los alumnos tienen dificultades para determinar cuál es la expresión correcta, o para verificar que lo sea cuando ya la hayan elegido, pídales que la utilicen con los valores de x y y que encontraron en la tabla anterior. Respuestas. La expresión algebraica correspondiente es xy = 24.

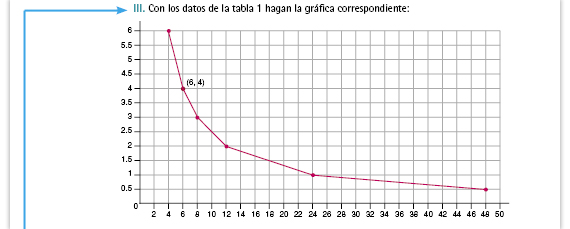
Respuestas. Deben graficar los puntos: (6, 4), (12, 2), (8, 3), (24, 1), (4, 6), (48, 0.5), y luego unirlos.

Respuestas. a) No puede medir 0 cm, lo que indica que la gráfica no pasa por el origen. b) No se puede porque no están sobre una recta. c) Las de proporcionalidad directa pasan por el origen y son rectas. Las de proporcionalidad inversa son hipérbolas y no pasan por el origen.

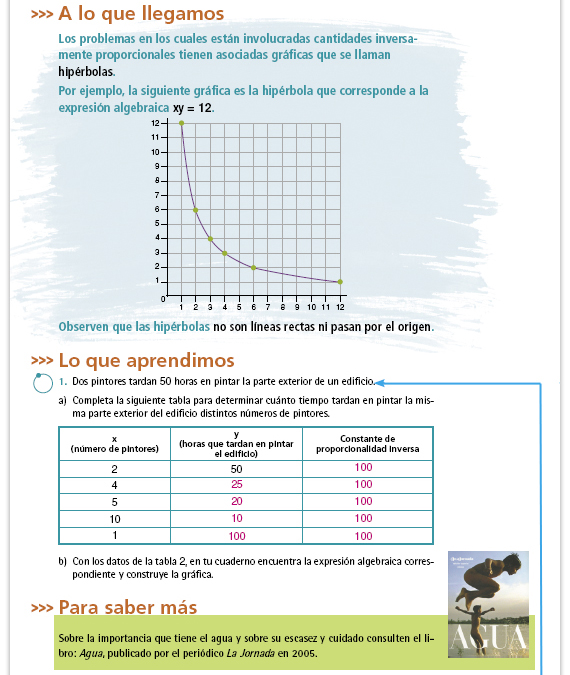
Integrar al portafolios. Guardar las respuestas de los alumnos a los incisos a) y b). Si considera que tienen dificultades repasen las actividades de Manos a la obra de las tres sesiones de esta secuencia. Respuestas. b) xy = 100 y también y=