3. Potencias grandes con ra�ces peque�as

La potenciaci�n y la radicaci�n

Manejo de potencias y ra�ces (ra�z cuadrada)

Profesor, en lo que respecta a la potenciaci�n el alumno se confunde y multiplica generalmente la base por el exponente en lugar de obtener la potencia, lo cual es incorrecto; para que se asimile la idea siga el siguiente procedimiento:

a) Aux�liese de una cartulina y recorte cuadros de 5 x 5 cm; en cada cuadro trace e ilumine un c�rculo del mismo color.

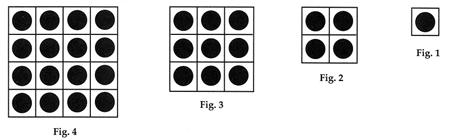
b) El procedimiento consiste en ir colocando los cuadros de cartulina de manera que se formen con �stos cuadros m�s grandes, obs�rvese las siguientes figuras.

Como se observa la fig. 2 est� formada por dos unidades por lado, la fig. 3 est� formada por tres unidades y la fig. 4 queda con cuatro unidades por lado, esto indica que si multiplicamos las unidades de cada lado se obtiene el total de cuadros que forman a cada figura.

fig. 1: 1 x 1 = 1� = 1

fig. 2: 2 x 2 = 2� = 4

fig. 3: 3 x 3 = 3� = 9

fig. 4: 4 x 4 = 4� = 16

Esto indica que para efectuar la potenciaci�n la base se toma como factor las veces que el exponente lo indique, tambi�n deber� tener en cuenta auxiliarse de los factores que al multiplicarse dan por resultado la potencia.

Para determinar la ra�z cuadrada de un n�mero, considere que la radicaci�n es la operaci�n inversa de la potenciaci�n, raz�n por la cual, cuando se trate de la ra�z exacta de un n�mero, explique que para determinarla se busca un n�mero que multiplicado por s� mismo d� el n�mero del cual se busca la ra�z. Cuando la ra�z del n�mero no sea exacta, determ�nela por estimaci�n.

Por �ltimo se le sugiere que mediante ejemplos sencillos el alumno utilice el c�lculo mental tanto en la potenciaci�n como en la radicaci�n.