II. TEMPERATURA Y TERMÓMETRO
¿POR CASUALIDAD pertenece usted, estimado lector; al grupo de personas que prefiere ponerse una chamarra cuando los demás están listos para vestir el traje de baño? ¿Se descubre todo lo posible en la noche, cuando las demás personas tienen frío aun bajo tres cobijas? En ese caso, sabe que los términos "frío" y "caliente" son relativos y específicos para cada persona.
Si no conoce experiencias como las mencionadas —lo cual es bastante improbable—
le invitamos a realizar un pequeño experimento que es sencillo y rápido: llene
tres recipientes grandes, uno con agua caliente (¡no tanto que pueda quemarse!),
uno con agua fría, y el tercero con agua tibia. Sumerja su mano en el recipiente
con agua caliente y la otra mano en el que contiene agua fría hasta que realmente
sienta calor y frío. Inmediatamente después sumerja ambas manos en el agua tibia:
sentirá el agua caliente en la mano que antes estaba en el agua fría y sentirá
el agua fría en la mano que sacó del agua caliente. Esta experiencia nos muestra
que, además de lo relativo de los términos "caliente" y "frío", nuestros sentidos
pueden engañarnos, ya que percibimos dos sensaciones diferentes de calor para
una misma temperatura.
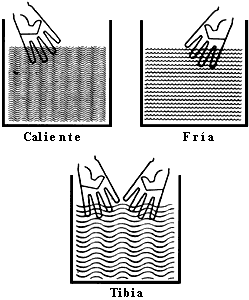
Figura 1. Nuestros sentidos pueden engañarnos.
Los experimentos han demostrado que somos capaces de percibir; a través de nuestro sistema nervioso, diferencias de temperatura muy pequeñas. Mediante el sentido del tacto, nuestra piel percibe diferencias de 0.1 grado. Lo que no podemos lograr es determinar, con nuestros sentidos, el valor absoluto de la temperatura de un cuerpo. Podemos sentir en forma cualitativa si un objeto está frío o caliente en relación con nuestro cuerpo, pero no podemos recordar, después de un tiempo, qué tan caliente o frío estaba dicho objeto. Tampoco podremos determinar cuál es la diferencia de temperatura de un cuerpo con respecto a otro.
Para poder realizar una comparación objetiva —o simplemente convencer a los amigos de que ponerse la chamarra está justificado— el hombre ha desarrollado un aparato de medición que no se deja engañar como nuestros sentidos. Este instrumento es el termómetro.
Algunos tipos de termómetro funcionan con base en el mismo principio físico: el hecho de que todas las sustancias —en mayor o menor medida— aumentan de tamaño con el calor y se contraen con el frío. A este fenómeno se le conoce como dilatación.
En la Grecia antigua se manejaban los conceptos de caliente y frío, y se realizaban experimentos simples que pueden considerarse, en forma retrospectiva, las bases de la termometría. Pero no fue sino hasta finales del siglo XVI (1592) cuando apareció el primer termoscopio, atribuido generalmente al científico italiano Galileo Galilei. Con este instrumento sólo podían obtenerse datos cualitativos, ya que carecía de una escala normativa que permitiese cuantificar las variaciones de temperatura. La idea de proveer al termoscopio con una escala y convertirlo así en un termómetro, se atribuye a Sanctorius Sanctorius, colega de Galileo, en 1611.
El gran médico de la antigŁedad, Claudio Galeno, a* escribía ya sobre la "medición" de la fiebre y no sobre la "sensación" de la fiebre. Hero de Alejandría b describía mediciones comparativas de la temperatura.
Así hemos llegado de nuevo al término temperatura, que requiere de una explicación detallada. Si consultamos un diccionario, encontraremos el siguiente tipo de definición:
"una medida para el estado calorífico de un sistema material." La traducción
de esta definición al lenguaje común expresa que la temperatura nos indica qué
tan "caliente" o qué tan "frío" está un cuerpo en un momento dado. Una manera
de entender el significado de "temperatura" es a través del contacto entre dos
cuerpos:
Si ponemos en contacto un cuerpo caliente con otro
frío, el material caliente le suministra energía, en forma de calor, al
material frío. El flujo de energía se detiene cuando ambos cuerpos tienen
el mismo valor de una propiedad, que es precisamente la que llamamos "temperatura".
Cuando dos o más cuerpos están en equilibrio térmico, es un requisito
que todos estén a la misma temperatura. Como el termómetro es un aparato
para medir la temperatura, si dos cuerpos están en equilibrio térmico,
el valor indicado por el termómetro deberá ser el mismo para ambos cuerpos.
|
Con lo anterior podemos introducirnos nuevamente en la historia; como ya mencionamos, Galileo Galilei c inventó el termoscopio, instrumento que consistía en un tubo lleno de agua o alcohol, abierto en su extremo inferior; y con una bola de vidrio llena de aire en el extremo superior. La parte abierta del tubo sobresalía hacia otro recipiente lleno de agua. Al calentarse la bola de vidrio se dilataba el aire interior; que a su vez empujaba el agua del tubo.
Muy pronto se descubrió que este "termómetro" tenía un funcionamiento limitado, ya que el aire —al igual que todos los gases— es fácilmente compresible, por lo cual con un pequeño calentamiento la presión opuesta de la columna de agua en el tubo de vidrio, es lo suficientemente grande para impedir una expansión visible del gas. Por esto se pensó, como alternativa, en los líquidos: en 1632 el francés Jean Rey d construyó un termómetro de agua.

Figura 2. Termoscopio de Galileo.
También esta solución tenía su talón de Aquiles: el agua, al ser calentada, no se dilata en forma lineal, es decir, en forma proporcional o uniforme. Otra desventaja del agua es que en los países fríos, durante el invierno, la temperatura ambiente puede bajar más allá de su punto de congelación.
Así se inicia la búsqueda de un líquido que, dentro de los límites de la temperatura del medio ambiente, no se congele ni se evapore y, además, cuya dilatación sea lineal. Los líquidos encontrados, el alcohol y el mercurio, constituyen el fundamento del termómetro actual. Aun así, no existían todavía las posibilidades de comparación, ya que cada descubridor utilizaba un "patrón" propio, es decir; tomaba puntos de referencia diferentes.
Imagínese usted un termómetro sin escala: con él podrían hacerse mediciones comparativas si se señalaran distintos puntos de referencia en el termómetro, pero no tendría usted una base para compararlos con el termómetro de su amigo, que seguramente habría marcado otros puntos distintos. Por ejemplo: Sanctorius marcó dos puntos, uno con el nivel del agua cuando el bulbo estaba rodeado de nieve derretida, y otro con el nivel alcanzado al calentar el bulbo con una vela. Después, dividió la distancia entre los dos puntos en 110 partes iguales.
En los inicios del siglo XVIII se utilizaban más de 30 escalas
diferentes de temperatura; muchas de ellas desaparecieron rápidamente y entre
las que prevalecieron destaca la del astrónomo danés Ole Romer e,
porque sirvió como base a Daniel Gabriel Fahrenheit para establecer su conocida
escala. Fahrenheit fijó dos puntos: uno que corresponde a la temperatura de
fusión del hielo, al que asignó un valor de 32; el otro punto fijo fue la temperatura
del cuerpo humano, a éste le asignó un valor de 96. Es digno de subrayar el
hecho de que la temperatura del cuerpo humano aceptada actualmente como normal
es de 98.6°F, valor muy cercano al determinado por Fahrenheit.
Es posible que usted, lector, piense que ésa es la escala Fahrenheit que se utiliza actualmente en los Estados Unidos, y con la cual usted tiene problemas para recordar su transformación a la escala que utilizamos en México. Sin embargo, la escala de Fahrenheit que se emplea en algunos países tiene como punto fijo superior el correspondiente a la temperatura de ebullición del agua al nivel del mar; y que es 212°F. En todo caso, reconocemos que no puede disminuirse la importancia de la contribución de Fahrenheit; en primer lugar porque construyó una escala dividida en partes iguales que por lo tanto eran comparables, y en segundo lugar porque su idea de tomar como punto cero la temperatura más baja no estaba desencaminada, ya que un siglo y medio después lord Kelvin retomó su idea.
En México utilizamos la escala inventada por el sueco Anders Celsius g, quien tomó como punto cero el punto de congelación del agua y como el otro extremo de referencia, 100 grados, su punto de ebullición; de este modo, dividió la escala en 100 partes iguales. Los mismos puntos escogió René-Antoine Ferchault de Réaumur h, sólo que él repartió la diferencia en 80 grados. Esta escala se utilizó hasta los años 30 de nuestro siglo en Europa; uno de los autores recuerda que en la casa de sus padres había un termómetro que tenía en la parte izquierda la escala de Celsius y en la derecha la de Réaumur.
Usted podrá decir, con razón, que la división a partir de los puntos de congelación y de ebullición del agua es tan arbitraria como las divisiones de Fahrenheit, y que uno podría elegir; a voluntad, el punto cero o un segundo punto de referencia. También podría pensar que la división en 100 grados es arbitraria; en términos del sistema decimal, ¿por qué no 10 grados o 1000?
Para la segunda pregunta existe una respuesta simple: los 100 grados sencillamente
han demostrado ser más prácticos. En la vida diaria basta esta división, ya
que da la aproximación suficiente para valores de la temperatura en números
enteros. Usted mismo habrá podido comprobar lo práctico de la escala Celsius
y lo complicado que es obtener; para una cierta temperatura, el valor correspondiente
en grados Fahrenheit. De hecho, es necesario aplicar la siguiente fórmula:
Así, para una temperatura de 100 °C corresponde un valor de 212°F y
para un valor de -17.77 °C tendremos prácticamente el cero de la escala
Fahrenheit.

Figura 3. Anders Celsius.
Respecto a la elección del punto cero, resulta interesante anotar que también el físico británico lord William Kelvin de Largs i contribuyó a la discusión sobre qué punto podría escogerse como punto cero. Partiendo de la idea de Fahrenheit, buscó establecer un punto de temperatura mínima. La diferencia fue que Kelvin determinó la temperatura mínima no a través de una mezcla frigorífica casual o una medida tomada al azar en un día muy frío, sino a través de cálculos que lo llevaron a la conclusión de que no puede existir una temperatura más baja que -273.15 grados Celsius.
|
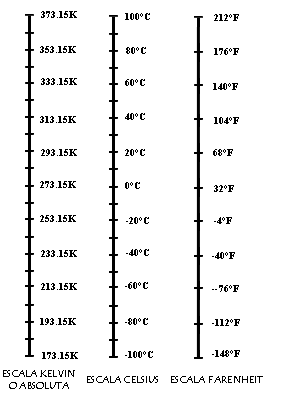
Cuadro 1. Escalas termométricas |
|
Así, Kelvin Colocó el punto cero de su escala de temperatura
en el punto cero absoluto. 1![]() Por
razones prácticas, conservó el tamaño de las divisiones fijado por la escala
Celsius y de esta manera el punto de congelación del agua es 273.15 K, mientras
que el punto de ebullición es 373.15 K. Tenemos así que una diferencia de
un grado Celsius (°C) equivale a una diferencia de temperatura de un Kelvin
(K).
Por
razones prácticas, conservó el tamaño de las divisiones fijado por la escala
Celsius y de esta manera el punto de congelación del agua es 273.15 K, mientras
que el punto de ebullición es 373.15 K. Tenemos así que una diferencia de
un grado Celsius (°C) equivale a una diferencia de temperatura de un Kelvin
(K).
A la escala de temperatura de Kelvin que en las ciencias es la única que
debe utilizarse, 2![]() comúnmente
se le llama escala de temperatura absoluta, ya que en lugar de tener
un punto de partida fijo y arbitrario (el punto cero), tiene un punto fundamentado
en la naturaleza de la materia. Por ello, la escala de Kelvin se distingue
de la mayoría de las unidades utilizadas en la física y la química.
comúnmente
se le llama escala de temperatura absoluta, ya que en lugar de tener
un punto de partida fijo y arbitrario (el punto cero), tiene un punto fundamentado
en la naturaleza de la materia. Por ello, la escala de Kelvin se distingue
de la mayoría de las unidades utilizadas en la física y la química.
Si usted reflexiona en lo arbitrario de la fijación del metro-patrón, que se utiliza para determinar longitudes, reconocerá que, en última instancia, la división no tiene en sí significado; lo importante es únicamente que todos sepan qué quiere decir una determinada unidad y cómo puede medirse. Las unidades de la física utilizadas comúnmente no son, por lo general, constantes dadas por la naturaleza, sino medidas fijadas arbitrariamente por el hombre, con las cuales todos sabemos cómo hacer una determinada medición.
Hemos visto ya cómo puede medirse la temperatura en diferentes escalas, pero todavía no sabemos de qué manera funciona un termómetro.
Hemos oído decir que la materia se dilata al calentarse y que esta dilatación no es siempre lineal. También sabemos que el alcohol y el mercurio fueron inicialmente los líquidos más utilizados para la construcción de los termómetros. Es claro que no todos los termómetros están construidos de esta manera, pero, ya que son los más usuales, comenzaremos por ellos: los termómetros de este tipo están constituidos por un tubo de vidrio con un diámetro interno muy pequeño (tubo capilar) soldado a una esfera de vidrio que contiene el líquido seleccionado. A mayor cantidad de líquido, la dilatación por calentamiento es más apreciable y por lo tanto el ascenso en el tubo capilar; más fácil de observar.
Seguramente usted habrá pensado que si los cuerpos se dilatan por el calor,
también se dilatará el vidrio en el cual está contenido el líquido. ¿Cambiará
este hecho la exactitud de la medición? La dilatación del vidrio del termómetro
es tan pequeña que podemos despreciarla; sólo para mediciones muy exactas debe
usarse otro tipo de métodos. Es importante considerar que por esta razón las
lecturas en el termómetro de vidrio tienen un margen de error de ![]() 0.01
K.
0.01
K.
Todos los líquidos se congelan y hierven a temperaturas específicas, por eso, cada termómetro está diseñado para determinados intervalos de temperatura. En el caso del mercurio, su punto de congelación es -39.0°C y el de ebullición es 356.7°C, valores que limitan su intervalo de aplicación. Por la misma razón, un termómetro de alcohol sólo funciona en un intervalo de -100°C a 70°C.
En general, los límites de uso de un termómetro de dilatación dependen de dos factores:
1) Los puntos de congelación y ebullición de los líquidos utilizados.
2) La temperatura de reblandecimiento del vidrio.
Cuando el líquido es el galio y el vidrio es de cuarzo, el intervalo de aplicación es de 35°C a 110°C.
En la calibración de los termómetros hemos dado por sentado que las temperaturas
de ebullición y congelación tienen el mismo valor bajo iguales condiciones.
Por desgracia, esto no es así. Aun bajo condiciones idénticas, el punto de congelación
del agua oscila ![]() 0.002
K y el de ebullición 0.01 K. j
0.002
K y el de ebullición 0.01 K. j
Usted podrá decir: ¡qué importan estas milésimas o centésimas!, ¡tanta exactitud no nos interesa! Para la vida diaria, tiene usted toda la razón, realmente sólo puede interesarle a un neurótico si el agua de la regadera está a 34 o a 34.02 grados. Pero para los científicos, y para muchos propósitos técnicos, la exactitud de un termómetro de vidrio no es suficiente; sin considerar que además muchas mediciones científicas y técnicas están fuera de los intervalos útiles de estos instrumentos.
Cuando se requiere una mayor exactitud, deben emplearse los termómetros que
aprovechan la sensibilidad a los cambios de resistencia eléctrica de ciertos
materiales. Por ejemplo, en los metales, al variar la temperatura cambia también
su conductividad eléctrica, es decir, cambia su resistencia al flujo de corriente
eléctrica. Con un sensor de temperatura como éste se pueden hacer mediciones
con una precisión de ![]() 0.001
K en un intervalo de 0°C a 400°C. Para trabajos todavía más precisos
se utilizan los termómetros de cuarzo, que tienen una exactitud de 0.0001 K
en un intervalo de -8°C a 250°C.
0.001
K en un intervalo de 0°C a 400°C. Para trabajos todavía más precisos
se utilizan los termómetros de cuarzo, que tienen una exactitud de 0.0001 K
en un intervalo de -8°C a 250°C.
Para medir temperaturas más altas o más bajas que las mencionadas, se utilizan elementos termoeléctricos (termopares) que se componen de dos metales diferentes, fácilmente soldables. Esta unión genera un potencial eléctrico que depende de la temperatura, y cuyo valor puede traducirse a una escala de temperaturas por medio de una tabla de calibración. Algunas uniones metálicas, como la de orocobalto, permiten mediciones desde un intervalo de unos cuantos Kelvin (poco más de 0 absoluto). La de tungsteno-tántalo puede utilizarse hasta 3 000 K (3273.15°C).
Cuando es necesario medir temperaturas mayores a 3 000 K, se deben utilizar métodos indirectos; por ejemplo, cuando se calienta el fierro empieza a ponerse incandescente (brillo sin llama), cambiando su color del rojo obscuro al blanco azulado. Un efecto parecido puede usted obtener en su casa con un regulador de intensidad de corriente que le permita observar el filamento de un foco. Conociendo esta corriente y la temperatura de incandescencia se puede asociar el color del filamento con su temperatura.
Estos son los métodos fundamentales para medir la temperatura, aunque no son, ni de lejos, los únicos. Un método muy importante para los científicos es el uso del termómetro que utiliza un gas en lugar de un líquido; de éste trataremos después de presentar algunos fundamentos necesarios para ello.
La termorrecepción es un proceso que realizan los seres vivos para detectar diferencias de temperatura.
La vida activa de los animales es posible dentro del estrecho intervalo que establece la temperatura de su cuerpo: entre 0°C y 45°C. Las limitaciones dependen del congelamiento de los tejidos a baja temperatura y de la alteración química de las proteínas del cuerpo, por encima del extremo superior de ese intervalo. Dentro de los límites establecidos, el metabolismo de un animal tiende a aumentar o disminuir paralelamente con la temperatura de su cuerpo.
En las especies más evolucionadas (aves y mamíferos), la temperatura del cuerpo y el metabolismo son relativamente independientes de las influencias térmicas directas del medio ambiente. Estos animales pueden mantener una considerable estabilidad fisiológica interna, aunque se den cambios en las condiciones ambientales y en las fluctuaciones climáticas y geográficas.
Por ejemplo, un oso polar puede realizar sus funciones normales durante el calor del verano, lo mismo que en las aguas frígidas del Ártico. Este tipo de flexibilidad está basada en estructuras sensoriales específicas llamadas termorreceptores, que le permiten al animal detectar los cambios térmicos y adaptarse a ellos.
En cambio, en las especies llamadas "de sangre fría", como los insectos, víboras y lagartijas, la temperatura ambiental se refleja directamente en la temperatura de su cuerpo, y por este motivo se mueven hacia zonas más favorables, como por ejemplo debajo de las piedras, en las zonas calientes. Los mosquitos, por otra parte, son atraídos por las radiaciones térmicas (infrarrojas) de sus huéspedes de "sangre caliente".
Las abejas normalmente escogen intervalos de temperatura entre 35°C ![]() 1.5°C.
1.5°C.
La sanguijuela puede discriminar temperaturas con una precisión de un grado Celsius. La babosa reacciona a temperaturas inferiores a 21°C, aumentando su actividad locomotora, y basta que la temperatura baje a 20.7°C para que, en un lapso de cinco minutos, haya cambiado su posición.
La antena de los mosquitos, donde probablemente se encuentra su termosensor, manifiesta una sensibilidad a los cambios en la temperatura del aire, de cerca de 0.5°C.
Algunas especies de peces, como el bacalao, nadan con la mitad de su cuerpo hacia afuera, como respuesta a cambios tan pequeños como de 0.03°C a 0.07°C en la temperatura del agua que los cubre.
Se considera que los termosensores de los peces están repartidos en la piel de todo el cuerpo. Sin embargo, en los anfibios sólo se ha registrado sensibilidad para cambios muy grandes de temperatura. Se ha publicado, por ejemplo, que una rana colocada en una sartén con agua fría no salta si el agua se calienta gradualmente. En efecto, se sabe que las ranas pueden permanecer quietas en esa agua hasta que mueren por cocimiento.
Los mamíferos y las aves tienen sus centros termorreguladores localizados principalmente
en el hipotálamo. La información que proveen dichos reguladores sirve para activar
mecanismos biológicos internos que mantienen la temperatura del cuerpo dentro
de los límites normales. Por ejemplo, la información de un aumento de temperatura
provoca mecanismos de pérdida de calor: sudoración, jadeo y vasodilatación en
la piel. Si las señales son de descenso de la temperatura se inician los mecanismos
de conservación del calor; mediante un movimiento muscular que consume energía
del organismo al tiritar, temblar; sacudirse, estremecerse y al producirse la
vasoconstricción.

Figura 4. Los gatos poseen termosensores en la nariz que les permiten responder a estímulos térmicos de 0.1 a 0.2 grados Celsius.
Las aves ahuecan el plumaje y los animales el pelo, para favorecer el aislamiento térmico. Todos estos cambios reguladores, involuntarios o automáticos, persisten durante la anestesia ligera o durante el sueño.
Un caso interesante son los termosensores que poseen los gatos en la nariz, receptores altamente específicos que responden a estímulos térmicos de 0.1 a 0.2°C. Esto corresponde a los niveles de sensibilidad térmica de la piel de la cara en los seres humanos.
¿Se ha preguntado, alguna vez, por qué la tubería por donde fluye el petróleo no es continua? ¿Se ha preocupado del aparente desperdicio de cables de luz, por la manera en que cuelgan entre los postes? ¿O se acuerda usted del monótono y fascinante "rat-tat-tat-tat" de los trenes cuando corren por los rieles? Todo esto, y muchas más cosas que usted habrá podido observar si va por el mundo con los ojos y los sentidos despiertos, tiene que ver con la dilatación, de la que algo hemos dicho en el capítulo anterior.
Con un experimento sencillo puede usted hacer visible este proceso en su casa. Coloque una aguja de acero de tejer en un cubo pequeño de madera (Figura 6a), de tal manera que aquélla no pueda moverse, y ponga en otro cubo de madera (de preferencia liso) una pequeña aguja de coser; en caso de que no tenga una madera lisa, coloque entre la aguja y la madera una hoja de rasurar limpia y libre de grasa. La aguja de coser debe sobresalir del cubo, para que pueda usted poner un pedacito de papel en la punta como detector (Figura 6b). Si usted calienta con un encendedor la aguja de tejer en la mitad, verá cómo empieza a girar el pedacito de papel (Figura 6c).
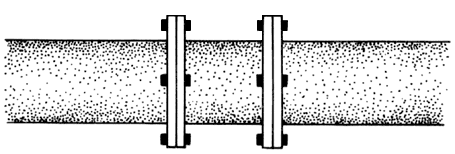
Figura 5a. Tubería con junta de expansión
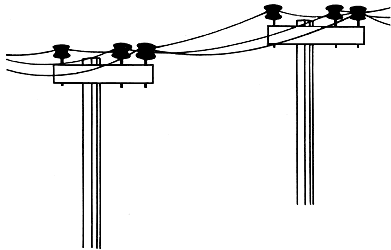
Figura 5b. Postes de luz donde se aprecia la holgura de los cables.
Un instrumento parecido se utiliza, en la práctica, en los institutos de física técnica, en los cuales se mide numéricamente la dilatación de diversos materiales. Usted se preguntará: ¿por qué es tan importante conocer cómo se dilatan los distintos materiales?
Esta pregunta puede contestarse con un pequeño ejemplo. Usted conoce, o ha oído hablar del famoso puente Golden Gate de San Francisco; una construcción de 1 280 m de largo que cruza el mar.
Supongamos que la temperatura en San Francisco, en el mes de enero, puede llegar hasta 12°C; y que en el verano puede llegar a 39°C. Consideraremos también, como factor de seguridad (margen de error), que las temperaturas pueden ser de hasta -20°C en invierno y hasta 45°C en verano.
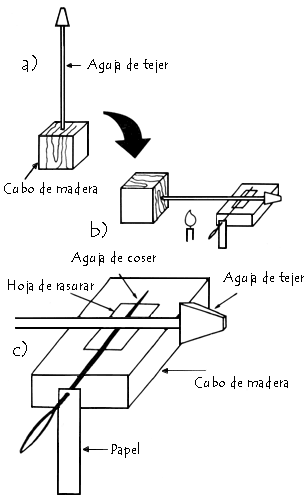
Figura 6 (a, b y c). Experimento sobre la dilatación de un metal.
Lo anterior quiere decir que el puente debe soportar diferencias de temperaturas
de 65K (o 65°C). Si hacemos los cálculos que normalmente realizan los ingenieros
constructores y consideramos una longitud de referencia, encontraremos que a
una temperatura -20°C el puente se acorta (o reduce) 61 cm. En el verano,
los cálculos indican que, para 45°C, el puente se alarga 39 cm.

Figura 7. El puente Golden Gate.
En total hay una modificación, entre los límites de la temperatura, ¡de 1 metro! Si los constructores de puentes no tomaran en cuenta la magnitud de la dilatación, la estructura se destruiría.
Los constructores de puentes no son los únicos que deben tomar en cuenta la dilatación térmica. En todo aquello en lo que las diferencias de temperatura intervengan en la técnica — y esto es en casi todos los campos— se debe considerar la dilatación. En los manuales de construcción podemos encontrar tablas que nos ayudan a estimar la dilatación de diversos materiales en función de los cambios de temperatura.
En ciertos intervalos, la dilatación es prácticamente lineal, es decir, que para cada grado que aumenta la temperatura de un cuerpo, éste se dilata o alarga en el mismo valor porcentual (este valor porcentual varía de acuerdo con el material en cuestión).
Para estimar la dilatación térmica lineal de un material en ocasiones podemos
utilizar la siguiente ecuación:
lt = l0 (l +at + bt2)
siendo l0 la longitud del material a 0°C y lt
la longitud a otra temperatura t.
|
C |

|
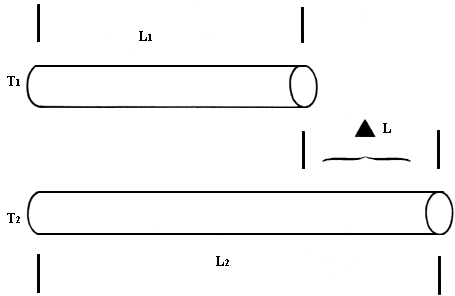
Figura 8 Dilatación lineal.
Considerar la dilatación de los cuerpos es, con frecuencia, un problema fundamentalmente técnico. Si tratáramos de impedir la dilatación sujetando fuertemente los extremos de un cierto material, veríamos que nuestro esfuerzo es en vano, ya que este efecto ocurre con una fuerza violenta. Al calentar una barra de acero de 5 mm de diámetro, aumentando su temperatura tan sólo un grado Celsius, la barra se dilata en una magnitud tal, que si deseáramos obtener el mismo efecto por esfuerzo mecánico, deberíamos colgar de la barra un peso de 2 600 kg, ¡más de 2.5 toneladas! (Figura 9.)
El talento humano no sólo ha logrado dominar técnicamente la dilatación cuando es indeseable, sino que ha ido más allá: la ha utilizado para su provecho.
Los puentes, cuando son largos, se dividen en segmentos que descansan a su vez sobre bases rodantes para permitir la libre dilatación. Entre los segmentos se dejan espacios para que puedan alargarse sin problemas.
Las construcciones de acero y concreto son posibles únicamente porque el concreto y el acero —¡por casualidad!— tienen el mismo coeficiente de dilatación longitudinal. Los tubos de cobre deben descansar libremente o ser colocados de tal manera que puedan dilatarse.

Figura 9. La dilatación ocurre con fuerza violenta.
El marcado colgado (combado) de los cables eléctricos es necesario para que,
en el caso de un invierno frío, los cables no se encojan tanto que puedan romperse
o hagan caer los postes.
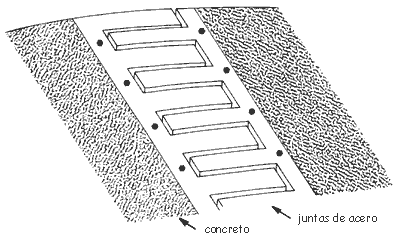
Figura 10. Estructura de acero y concreto.
Ya en la Edad Media se usaba una técnica interesante: sobre las ruedas de madera
de las carretas se clavaba una banda de hierro calentado para que al enfriarse
se encogiera y, bajo condiciones normales, no pudiera desprenderse la rueda.
Con la misma técnica, un poco más "elaborada", se fabrican las ruedas de los
trenes: la pestaña se calienta entre 600°C y 800°C para que ajuste al
buje. Al encogerse por enfriamiento, las uniones entre la pestaña y el buje
son prácticamente indisolubles. Por el contrario, los tornillos que están pegados
pueden separarse sumergiendo la cabeza del tornillo en agua caliente: la dilatación
provocada por el calor es suficiente para que se puedan despegar.
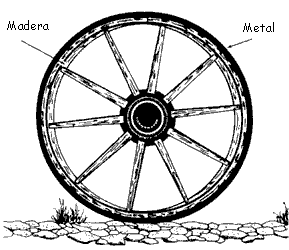
Figura 11. Rueda de carreta.
Así pueden encontrarse miles y miles de ejemplos en los cuales la dilatación tiene un papel importante. Seguramente no será difícil para el lector dar con ejemplos de lo anterior en su vida cotidiana.
Usted podrá decir; con razón, que hasta ahora sólo se ha hecho referencia a las sustancias y cuerpos sólidos. ¿Pero qué sucede con los líquidos y los gases? y sobre todo, ¿qué pasa con el agua, si en el capítulo anterior se afirmó que no presenta una dilatación lineal? Estas preguntas se hallan totalmente justificadas: tanto los líquidos como los gases se dilatan. La dilatación de los líquidos es, por lo general, mayor que la de los sólidos. En cuanto a que el agua no se dilate linealmente, esto tampoco es una excepción. Lo que sucede es que es mucho más notoria en intervalos de temperatura fácilmente observables.
Si usted no vive en un clima muy extremoso quizá nunca se haya preguntado cómo pueden sobrevivir los peces cuando se congelan los ríos o los lagos. La respuesta está precisamente en esa anomalía que presenta el agua con respecto a su dilatación: Si se calienta lentamente agua congelada a 0°C, se puede demostrar que su volumen inicialmente disminuye, a pesar de que normalmente el calentamiento debería producir una dilatación y ésta ir acompañada de un aumento de volumen. Hasta 4°C, el volumen del agua disminuye y, a partir de esta temperatura, empieza a aparecer la dilatación.
Aun con una disminución pequeña de volumen, existe un cambio en la densidad
3![]() y
como el agua líquida resulta más densa que el hielo, sólo se congela la superficie
de los lagos y los ríos.
y
como el agua líquida resulta más densa que el hielo, sólo se congela la superficie
de los lagos y los ríos.
¿Todas las sustancias muestran esta anomalía? Sí, estimado lector; todas la presentan, aun cuando, como ya se mencionó, no siempre en intervalos fácilmente observables. Muy frecuentemente deja de presentarse la disminución de volumen por calentamiento que se aprecia en el caso del agua, y lo que se presenta es un escaso aumento de la dilatación. Un ejemplo muy ilustrativo de esto ocurre en el fierro, donde la anomalía aparece a 720°C.
CUADRO 3. En los gases y en los líquidos, la dilatación se mide por un aumento en el volumen. Una excepción es el agua, cuyo volumen disminuye al aumentar la temperatura de 0°C a 4°C. Después de esta temperatura, el agua se dilata normalmente.
El coeficiente de expansión térmica a presión constante (av) se define por la expresión:
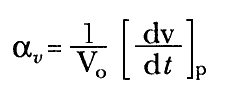
Algunos valores publicados para gases son:
|
|
|
|
|
|
|
|
|
| Aire |
|
| Helio |
|
| Hidrógeno |
|
| Nitrógeno |
|
|
|
|
En el caso de los líquidos, su expansión cúbica puede calcularse con la fórmula:
Algunos valores publicados y válidos para temperatura ambiente (25°C) son:
|
|
|||
|
|
|
|
|
|
|
|||
| Acetona |
|
|
|
| Cloroformo |
|
|
|
| Aceite de oliva |
|
|
|
| Agua |
|
|
|
|
|
|||
¿No está rondando por su cabeza la pregunta de por qué se dilatan los cuerpos y por qué los líquidos más que los sólidos?
La respuesta descansa en la propia estructura de la materia. Es importante señalar que, en este sentido, también fueron los griegos los primeros en buscar una explicación de la estructura de la materia. La encontraron de una manera sorprendentemente moderna, aunque sólo tenía una base especulativa sin experimentación ni complejos microscopios electrónicos, ni aceleradores de partículas.

Figura 12. Demócrito.
El filósofo griego Demócrito k propuso que las diferentes sustancias estaban formadas por partículas muy pequeñas, invisibles e indivisibles, que llamó átomos (del griego átomos = indivisible). De acuerdo con el pensamiento griego de ese tiempo, asignó representaciones geométricas distintas para cada sustancia. Durante un siglo éstas fueron las ideas que prevalecieron en los griegos cultos, sin que ninguno considerara la posibilidad de demostrarlas mediante experimentos, lo cual no les parecía necesario, ya que para ellos era suficiente que fuera en sí una idea completa que pudiera comunicarse brillantemente. La ciencia era la confrontación con el contenido del pensamiento, sin que se exigiera una comprobación experimental para contrastarlo con la realidad. Con ello se puede entender que la ciencia fuera para ellos una parte de la filosofía, una parte del amor a la sabiduría.

Figura 13. Aristóteles.
Así, no fue difícil para el filósofo griego más conocido, en lo que actualmente llamamos filosofía y cuyas ideas tienen hoy la misma validez que hace 2 400 años, triunfar con sus ideas "científicas" contra la teoría atómica de Demócrito. Por supuesto nos referimos a Aristóteles Por más de dos mil años las ideas de Aristóteles frenaron el desarrollo de la ciencia, ya que si sus consideraciones filosóficas eran irrebatibles, ¿cómo no iban a serlo las científicas?
La negación de la observación y la experimentación en sus escritos fundamentaron entre otras la convicción (o creencia) de la existencia de cuatro elementos: fuego, agua, tierra y aire. Como estos trabajos corrían paralelos con sus incuestionables trabajos de lógica, los griegos y sus descendientes sacrificaron durante siglos el desarrollo del pensamiento científico, tal y como hoy día lo entendemos. Para dar un pequeño ejemplo drástico de sus suposiciones, vale la pena mencionar que Aristóteles sostenía que las mujeres tenían menos dientes que los hombres. Como además la Iglesia apoyó de manera decisiva sus escritos, sus críticos eran considerados como detractores de Dios. Las primeras dudas sobre la existencia de los cuatro elementos aparecieron en el Renacimiento, con Giordano Bruno, m Galileo Galilei, sir Isaac Newton n y Christian Huygens,0 entre otros.
Finalmente, se aceptó que la materia estaba formada por moléculas, a su vez
constituidas por átomos indivisibles, una idea que el mundo debe agradecer al
inglés Robert Boyle.p Estas ideas de Boyle tampoco
estaban sustentadas en experimentos, por lo que fueron tomadas por sus contemporáneos
como "fantasías".

Figura 14. Galileo Galilei.
Casi cien años después, el suizo Daniel Bernoulli q pudo comprobar que la presión de un gas era simplemente el resultado de las colisiones de las moléculas del gas con la pared del recipiente que lo contenía. Al mismo tiempo, Bernoulli consideró que la presión de un gas debía ser proporcional al promedio de la velocidad al cuadrado de cada una de las moléculas, lo cual fue comprobado experimentalmente por Robert Hooke, r Rudolf Clausius, s James C. Maxwell t y Ludwig Boltzmann. u Con ello se dio la fundamentación para que Albert Einstein v desarrollara su teoría de la relatividad.
También se continuaron los estudios sobre la estructura del átomo. Sin embargo, sólo nos ocuparemos del concepto de molécula, el cual es suficiente para entender; de manera sencilla, los fenómenos relacionados con la dilatación. Una molécula es la unidad más pequeña de una sustancia, que conserva sus propiedades. Las moléculas pueden ser monoatómicas o estar formadas por dos o más átomos.

Figura 15. Isaac Newton.

Figura 16 (a). Chiristian Huygens.
Las moléculas pueden estar formadas por el mismo tipo de átomos o por átomos de diferentes tipos.
No vamos a considerar aquí la manera como las moléculas están estructuradas internamente (fuerzas intramoleculares); lo que nos interesa es la unión de las moléculas entre sí (fuerzas intermoleculares). Las fuerzas intermoleculares son las que determinan si un material se encuentra en estado líquido o sólido, el valor de su temperatura de ebullición, etcétera.

Figura 16 (b). Robert Boyle.
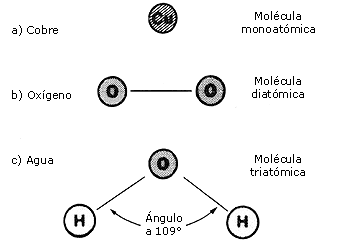
Figura 17 (a, b y c). Las moleculas pueden ser monoatómicas, diatómicas, triatómicas y poliatómicas.
En el caso de los sólidos podemos encontrar dos grandes grupos: los materiales cristalinos y los amorfos. Cuando los átomos están ordenados en estructuras cristalinas, constituyen redes que cumplen rigurosamente con las leyes de la geometría. La manera más fácil de apreciar esto es en algunas muestras de minerales donde a simple vista se pueden observar las formas geométricas que toman los cristales. Por otra parte, debemos recordar que en la realidad es casi imposible tener un cristal perfecto, y casi siempre se presentan defectos cristalinos, esto es, zonas en las que parece romperse la continuidad del cristal, o bien puntos de la red donde falta un átomo.
De manera muy simplificada se puede decir que las fuerzas de unión dependen de si en el cristal los puntos de la malla están ocupados por moléculas, radicales, iones o átomos. Una descripción detallada de las uniones químicas está fuera del marco de este libro; sin embargo, sólo se desea subrayar que de ellas dependen muchas de las propiedades físicas de los cuerpos: la elasticidad, plasticidad y conductividad, entre muchas otras.
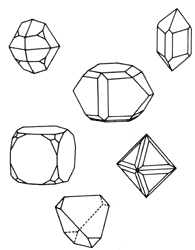
Figura 18 estructuras cristalinas.
Un ejemplo interesante resulta de comparar los diamantes y el grafito con que está hecha la punta de su lápiz. Ambos materiales están formados exclusivamente por átomos de carbono; sus propiedades fisicoquímicas tan diferentes se deben al tipo de unión entre los átomos.
|
|
|
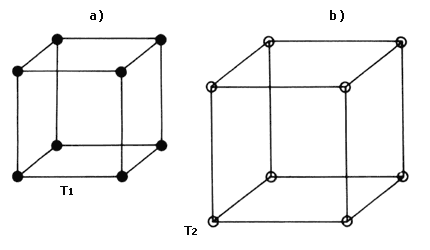
Figura 19a. Cristal antes del calentamiento. |
Figura 19b. Cristal después del calentamiento. |
Para continuar con nuestra explicación, imaginemos un arreglo geométrico en forma de un cubo cuyos vértices están ocupados por pequeñas esferas que representan a los átomos (ver figura 19). De esta manera tenemos un modelo muy simple de un cristal. Cada esfera, cada átomo, está vibrando respecto a un punto fijo (vibración de la malla cristalina). Sigamos imaginando que las esferas están unidas —según la sustancia será la fuerza— por ligas que representan las fuerzas de unión entre ellas. La actuación de estas fuerzas es tal que los átomos no pueden moverse uno con respecto al otro (es decir; alejarse o acercarse) sino que se mantienen vibrando en posiciones fijas. Si calentamos el cubo, los átomos empezarán a vibrar más rápidamente. Al mismo tiempo, las fuerzas entre los átomos serán menores, de tal manera que al cubo le sucede lo que a las ligas de hule: se ablandan y se hacen más flexibles cuando se calientan. El resultado de lo anterior es que el cubo se hace más grande, es decir; se dilata.
Ahora bien, ¿por qué se dilatan en mayor proporción los líquidos que los sólidos?
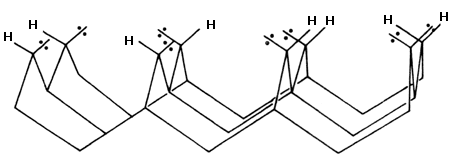
Figura 20. Modelos de un líquido. (Doctor F. J. Garfias.)
Volvamos a nuestro cubo. Si continuamos calentándolo, los movimientos de los
átomos serán cada vez más rápidos, y las fuerzas de unión serán más débiles.
Así, llega un momento en el que las fuerzas ya no son lo suficientemente grandes
para mantener unidos a los átomos o a las moléculas. El sólido se funde y
se transforma en un líquido. Los líquidos no tienen una estructura cristalina
(aquí no vamos a hablar de lo que los físicos llaman cristales líquidos),
4![]() y las fuerzas que unen a los átomos o a las moléculas
son más débiles que en los sólidos. Algunos científicos mexicanos, como el
doctor Francisco Javier Garfias, han investigado los líquidos y planteado
que algunos, como el caso del agua, mantienen una cierta estructuración, y
las moléculas forman grupos o "agregados" (ver figura 20).
y las fuerzas que unen a los átomos o a las moléculas
son más débiles que en los sólidos. Algunos científicos mexicanos, como el
doctor Francisco Javier Garfias, han investigado los líquidos y planteado
que algunos, como el caso del agua, mantienen una cierta estructuración, y
las moléculas forman grupos o "agregados" (ver figura 20).
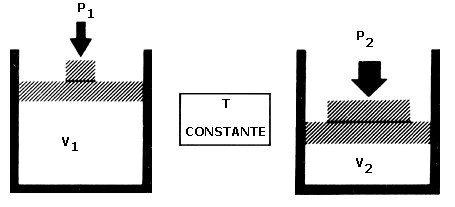
Figura 21. Ilustración de la ley de Boyle-Mariotte.
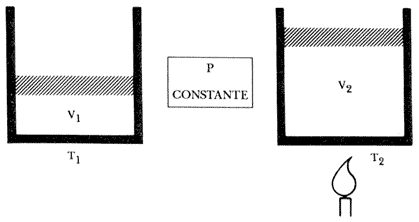
Figura 22. Ilustración de la ley de Charles-Gay Lussac.
¿Qué sucede al respecto con los gases?
Los gases no tienen volumen propio, sino que éste depende de la temperatura y la presión a que sean sometidos. Si mantenemos la presión constante, el volumen de un gas aumentará conforme aumente la temperatura. Por otra parte, si mantenemos la temperatura constante y aumentamos la presión, disminuirá el volumen del gas en proporción inversa al aumento de la presión. Estas relaciones son comunes a todos los gases sin importar la naturaleza de los mismos.
De lo anterior; el conde italiano Amadeo Avogadrow concluyó que para igual temperatura e igual presión, gases diferentes tendrían el mismo volumen y por lo tanto tendrían que tener también el mismo número de moléculas dentro de ese volumen. Otra manera de decir esto es afirmar que si las condiciones de presión y temperatura son constantes, "iguales volúmenes de diferentes gases contienen el mismo número de moléculas".
A través de mediciones y cálculos específicos Joseph Lodschmidt x determinó por primera vez la llamada constante de Avogadro: 6.022045 x 1023 moléculas están contenidas en 22.4 l de un gas ideal a 0°C y 760 mm Hg.
Más adelante explicaremos a qué llamamos un gas ideal. Primero hagamos un pequeño cálculo aritmético. A partir de la constante de Avogadro se puede calcular que en cada centímetro cúbico (un mililitro) de cualquier gas ideal están contenidas a la presión de 760 mm Hg (una atmósfera) y a la temperatura de 0°C o 273.15 K un total de 2.6884 x 1019 moléculas (veintiséis trillones, ochocientos ochenta y cuatro billones de moléculas). Este número supera la capacidad de imaginación del hombre: si alguien quisiera contar este número de moléculas, a un ritmo de 10 moléculas en un segundo, tardaría, sin pausas, más de ochenta y cinco mil millones de años en poder hacerlo. Empiece de una vez para terminar pronto! Naturalmente, Lodschmidt no las contó una por una, sino que obtuvo esta cantidad a través de cálculos matemáticos.

Figura 23. Si alguien quisiera contar las moléculas que hay en 1 cm3 de gas, tardaría en hacerlo mas de 85 mil millones de años.
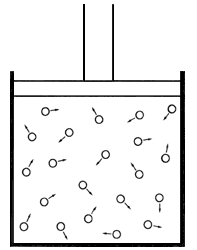
Figura 24. Esquema molecular de un gas.
La estructura molecular de los gases es la siguiente: un gas está constituido por moléculas muy separadas unas de otras —respecto al diámetro de una de ellas, tomado como unidad de medida— por lo cual prácticamente no existen fuerzas de unión entre ellas. Estas moléculas, se ha comprobado experimentalmente, se mueven desordenadamente a grandes velocidades.

Figura 25. Movimiento browniano.
La consideración del movimiento caótico (al azar) de las partículas proviene de la biología y no de la física. El botánico inglés Robert Brown y descubrió, a través del microscopio, que el polen espolvoreado sobre una superficie líquida se movía en zigzag al azar. A pesar de la deficiente explicación que él dio a este fenómeno: "el polen está vivo, es decir es orgánico", posteriormente se comprobó que también las partículas inorgánicas presentan este tipo de movimientos. El primero que encontró una explicación a este fenómeno, denominado "movimiento browniano", fue Einstein, quien comparó dicho movimiento con el de las bolas de billar; con las cuales podemos simular las colisiones de las partículas entre sí y contra las paredes del recipiente.
¿Existe relación entre el movimiento de las partículas y el fenómeno de la dilatación?
El movimiento browniano de las partículas contenidas en un gas o en un líquido, se hace más caótico y más rápido cuando éstos son calentados.
Podemos imaginar un gas como un gran número de mcoléculas en movimiento caótico constante. Cada partícula viaja en línea recta a gran velocidad; en su trayecto puede chocar con otras partículas o con las paredes del recipiente. A medida que el gas se calienta, las moléculas se mueven más rápidamente y por lo tanto las colisiones son más frecuentes. Debido a lo anterior; las moléculas tienden a ocupar un volumen mayor: el gas se dilata.
Llamamos gases ideales a aquellos cuyo comportamiento puede describirse adecuadamente
con la siguiente ecuación, llamada por esto ecuación del gas ideal,
que relaciona los términos de presión, temperatura y volumen de un número n
de moles gaseosas:
Con esta ecuación podemos calcular que la dilatación es igual para todos los gases ideales: 1/273.15 de su volumen por cada grado que se eleve su temperatura a presión constante. En el siguiente capítulo explicaremos con más detalle la ecuación del gas ideal.