Propósito de la sesión. Explicitar las principales características del sistema de numeración decimal. Organización del grupo. Casi toda la sesión se trabaja de manera individual, excepto una actividad en equipos y los intercambios grupales. Es probable que para esta sesión se requieran dos clases.

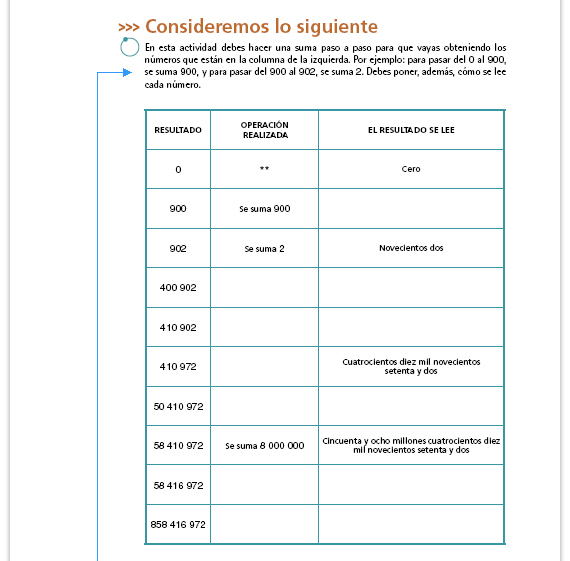
Propósito de la actividad. La intención es que los alumnos ubiquen cada cifra en el valor de posición que le corresponde, comprendiendo así que, para pasar del 403 al 473, por ejemplo, no hay que sumar 7 sino 70. Sugerencia didáctica. Si tienen calculadora puede sugerirles que la usen para verificar sus respuestas.

Sugerencia didáctica. Si lo considera pertinente, pida a algunos alumnos que pasen al pizarrón a escribir cómo lo resolvieron.

Sugerencia didáctica. Comente con los alumnos que en esta tabla se les llama "Unidades" a las centenas, decenas y unidades sólo para la lectura de los números.

Sugerencia didáctica. Pida a los alumnos que investiguen si existen números mayores que los billones y cómo se escriben.

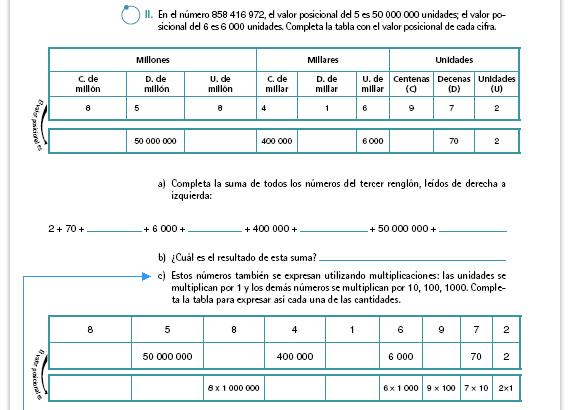
Sugerencia didáctica. Esto ya se ha visto alguna vez en la primaria, pero es posible que algunos alumnos no lo recuerden. Si tienen dificultades pueden resolverlo en el pizarrón explicando las multiplicaciones.

Propósito de las preguntas. La idea es que los alumnos reconozcan que una cifra puede tener distinto valor dependiendo de dónde se escriba. Las dos preguntas deben responderse en grupo.

Integrar al portafolios. El valor posicional es un concepto central en esta secuencia. Usted podrá tener información de lo que saben los alumnos al respecto a través de esta actividad. Si nota que aún tienen dificultades propóngales actividades parecidas Respuestas a) 0 b) 0 c) Hay dos maneras de resolver esta actividad. Por lo que han venido haciendo, la que se espera es: 2 × 1 + 7 × 10 + 9 × 100 + 0 × 1 000 + 1 × 10 000 + 4 × 100 000 + 0 × 1 000 000 + 5 × 10 000 000 × Aunque también puede expresarse como: 2 × 1 + 7 × 10 + 9 × 100 + 1 × 10 000 + 4 × 100 000 + 5 × 10 000 000

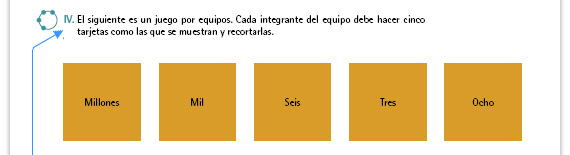
Sugerencia didáctica. Cada alumno necesita su juego de tarjetas para poder explorar las posibles combinaciones.

Respuestas. Hay 12 distintos números que pueden formarse con las tarjetas: 8 006 000 003; 8 003 000 006; 6 008 000 003; 6 003 000 008; 3 008 000 006; 3 006 000 008; 8 006 003; 8 003 006; 6 008 003; 6 003 008; 3 008 006; 3 006 008 Sugerencia didáctica. Pida a un equipo que escriba en el pizarrón los números que encontraron. Los demás equipos deben observar si ellos tienen los mismos números, y si no es así, anotar en el pizarrón aquellos que falten.

Sugerencia didáctica. Pida a los alumnos que copien esta información en una cartulina o papel para pegarlo en el salón.

Propósito de la actividad. Que los alumnos escriban con letra números hasta millones y que presenten datos en tablas de manera ordenada.

Propósito de la actividad. Se pretende que los alumnos identifiquen las propiedades más importantes de cada uno de los sistemas de numeración.

Sugerencia didáctica. En el Fichero de Actividades Didácticas, de donde se toma la actividad de las tarjetas, se comenta que al agregar la de la palabra ciento(s) el número de combinaciones posibles aumenta considerablemente. Por esta razón, conviene establecer un tiempo límite para la actividad, o bien, poner algunas restricciones, por ejemplo, encontrar los mayores a mil millones o los menores a diez millones. Si lo considera conveniente, esta actividad puede desarrollarse en equipos. Respuestas. El número mayor es el 806 003 000 000 (ochocientos seis mil tres millones). El menor es el 3 006 108 (tres millones seis mil ciento ocho).