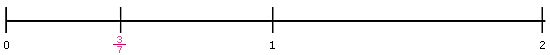|

|

|
 |
 |

| Propósito de la sesión. Resolver
problemas de comparación de
números fraccionarios usando la recta
numérica como un recurso. Reconocer
la conservación de la escala y la
arbitrariedad de la posición del cero.
Organización del grupo. En la sesión el trabajo es individual y en parejas, con momentos para la discusión grupal. |
| Eje |
| Sentido numérico y pensamiento algebraico. |
| Tema |
| Significado y uso de los números. |
| Antecedentes |
| En la escuela primaria los alumnos resolvieron problemas que implicaban comparar y ordenar números decimales y fraccionarios. En esta secuencia resolverán situaciones en las que se utiliza la recta numérica como un recurso que permite dar sentido a los números fraccionarios y a los números decimales. |
| Propósitos de la secuencia
Representar números fraccionarios y decimales en la recta numérica a partir de distintas informaciones, analizando las convenciones de esta representación. |
||
| Sesión | Propósitos de la sesión | Recursos |
| 1 | El salto de altura
Resolver problemas de comparación de números fraccionarios usando la recta numérica como un recurso. Reconocer la conservación de la escala y la arbitrariedad de la posición del cero. |
Video "El salto de altura" |
| 2 | Densidad y fracciones Resolver problemas de densidad de números fraccionarios usando la recta numérica como un recurso. | Interactivo |
| 3 | El salto de longitud y los números decimales Resolver problemas de comparación y densidad de números decimales usando la recta numérica como un recurso. Reconocer la conservación de la escala y la arbitrariedad de la posición del cero. | Interactivo |
| Propósito del video. Contextualizar el uso y la comparación de números fraccionarios representados en la recta numérica. |
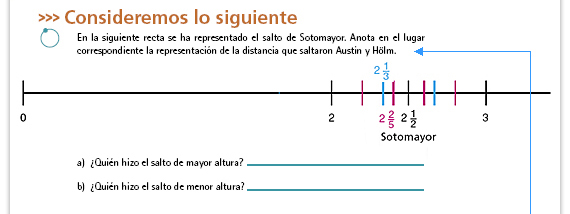
| Propósito de la actividad. Comparar
números fraccionarios usando la
recta numérica como un recurso. Para
ubicar un número fraccionario en la
recta numérica, los alumnos deberán
establecer dos aspectos fundamentales:
asignar el cero a un punto de la recta y
la escala.
Posibles procedimientos. Un procedimiento posible para ubicar las fracciones 2 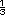 y 2 y 2 es localizar primero
el 3 y dividir el segmento que va del
2 al 3 en partes iguales (quintos y
tercios) para finalmente tomar las partes
necesarias. es localizar primero
el 3 y dividir el segmento que va del
2 al 3 en partes iguales (quintos y
tercios) para finalmente tomar las partes
necesarias.
Para localizar el 3 hay que conservar la escala con la que está construida la recta numerica. Algunos alumnos pueden ubicarlo de manera arbitraria a la derecha de 2  , sin considerar la escala.
Es muy importante que en este momento
no los corrija, pues mas adelante tendran
oportunidad de verificar sus respuestas.
Un posible procedimiento correcto para
localizar el 3 consiste en usar la longitud
del segmento que va de 2 a 2 , sin considerar la escala.
Es muy importante que en este momento
no los corrija, pues mas adelante tendran
oportunidad de verificar sus respuestas.
Un posible procedimiento correcto para
localizar el 3 consiste en usar la longitud
del segmento que va de 2 a 2 como
unidad y localizar el 3 a la derecha de 2 como
unidad y localizar el 3 a la derecha de 2  y a la misma distancia que 2.
y a la misma distancia que 2.
Otro procedimiento correcto consiste en localizar el 1 (como el punto medio del segmento que va de 0 a 2) y usarlo como unidad para localizar el 3. Recomiende a sus alumnos que usen lápices de colores para evitar confusiones entre los tercios y los quintos. |

| Sugerencia didáctica. Elija al menos
dos soluciones distintas para poder
compararlas.
Un posible error al ordenar las alturas es que los alumnos consideren que 2  es mayor que 2 es mayor que 2 o que 2 o que 2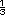 ,
"porque 5 es mayor que 2 y que 3" si se fijan en
los denominadores, o tambien porque
"2 es mayor que 1" si se fijan en los
numeradores. En este momento no los
corrija, en la seccion Manos a la obra
podran identificar dichos errores. ,
"porque 5 es mayor que 2 y que 3" si se fijan en
los denominadores, o tambien porque
"2 es mayor que 1" si se fijan en los
numeradores. En este momento no los
corrija, en la seccion Manos a la obra
podran identificar dichos errores. |

 Sugerencia didáctica. Pregunte
a los alumnos qué procedimiento
utilizaron para ubicar una fracción
en la recta. Después de que lean con
cuidado el procedimiento de la hoja
rayada pregúnteles si ya lo conocían
y si alguien lo utilizó para resolver las
actividades anteriores.
Sugerencia didáctica. Pregunte
a los alumnos qué procedimiento
utilizaron para ubicar una fracción
en la recta. Después de que lean con
cuidado el procedimiento de la hoja
rayada pregúnteles si ya lo conocían
y si alguien lo utilizó para resolver las
actividades anteriores. |
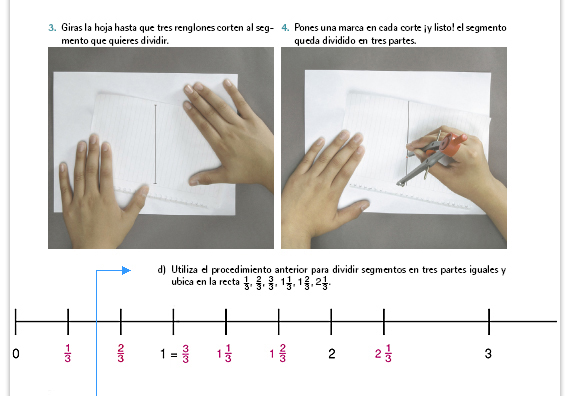
| Sugerencia didáctica. Recuerde a los alumnos que un número es mayor que otro si está más a la derecha en la recta numérica. |

| Sugerencia didáctica. Este es un buen momento para corregir los errores que los alumnos hubieran podido cometer al inicio de la sesión. |
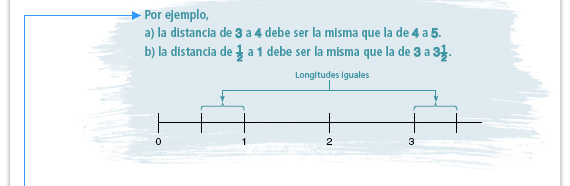
| Para recordar. Esta conservación de la distancia (a diferencias iguales entre números deben corresponder distancias iguales en la recta), es la conservación de la escala de la recta numérica. |

| Propósito de la actividad. Se
pretende que los alumnos reconozcan
que un solo punto de la recta numérica
no define la escala, de modo que
este problema tiene una infinidad de
soluciones.
Posibles procedimientos. Probablemente los alumnos traten de ubicar el número 1 primero. El 1 puede ser colocado a cualquier distancia del 0 (la escala aun no esta definida), pero el número 2 debe estar colocado a una distancia igual con respecto al 1 que la que hay entre el 0 y el 1. Posteriormente hay que dividir en tercios para ubicar la fraccion que se indica. El 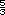 se encuentra
entre el 1 y el 2. Tambien puede
convertirse a número mixto (1 se encuentra
entre el 1 y el 2. Tambien puede
convertirse a número mixto (1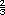 ). ).
Otra forma de resolver es colocando el 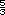 en cualquier punto de la recta. Si
los alumnos lo hacen asi, pidales que
localicen entonces el 1 y que comparen
el tamano de los segmentos que van del
0 al 1. en cualquier punto de la recta. Si
los alumnos lo hacen asi, pidales que
localicen entonces el 1 y que comparen
el tamano de los segmentos que van del
0 al 1.
Posiblemente sea dificil para los alumnos entender que 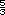 puede
ubicarse en cualquier punto porque
probablemente en las rectas numericas
que han conocido se marcan al menos
dos números, y con referencia a ellos se
ubica a un tercero (como en la recta B). puede
ubicarse en cualquier punto porque
probablemente en las rectas numericas
que han conocido se marcan al menos
dos números, y con referencia a ellos se
ubica a un tercero (como en la recta B).
Sugerencia didáctica. Hágales notar que una vez definida la escala (con dos puntos), ésta debe conservarse para localizar más puntos de la recta. |
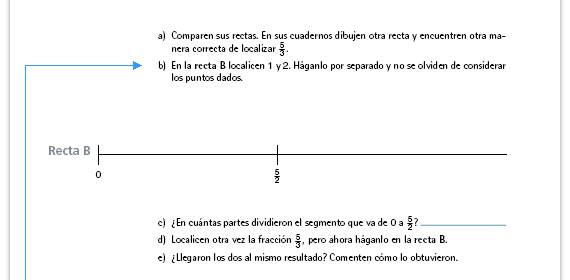
| Propósito de la actividad. El
propósito en este problema es reconocer
que dos puntos de la recta numérica
definen la escala.
Sugerencia didáctica. Si los alumnos tienen dificultades en esta actividad puede sugerirles que utilicen la hoja rayada. Si la colocan de manera que el segmento  quede dividido en cinco
partes iguales tendran cinco segmentos
de quede dividido en cinco
partes iguales tendran cinco segmentos
de  cada uno. cada uno. |

Propósito de las preguntas. Lo
importante es que concluyan que en la
recta A el punto 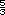 se puede ubicar de
infinitas maneras, mientras que en la
recta B solo hay una manera de hacerlo
correctamente se puede ubicar de
infinitas maneras, mientras que en la
recta B solo hay una manera de hacerlo
correctamente |

Respuestas. Para ubicar correctamente
los puntos en las rectas es necesario
que el alumno considere la escala y
luego que divida en tantas partes como
indique el denominador de la fraccion
que va a ubicar. Por ejemplo, en el inciso
a) debe considerar que  < 1 y que, por
lo tanto, < 1 y que, por
lo tanto,  esta entre 0 y 1; despues
debe fraccionar el segmento del 0 al 1
en cinco partes (cada una de tamaño esta entre 0 y 1; despues
debe fraccionar el segmento del 0 al 1
en cinco partes (cada una de tamaño 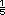 )
para asi hallar el número )
para asi hallar el número  . .
En estos incisos la escala ya está definida, pues se dan al menos dos puntos de la recta numérica. Integrar al portafolios. Pida a los alumnos que en una hoja aparte, copien y resuelvan dos de los incisos del número 1, dos del 3 y que ubiquen dos fracciones del número 2. Si aún cometen errores en la localización de fracciones en la recta, revise con ellos la sección Manos a la obra y hagan ejercicios parecidos en el pizarrón. |
Respuestas.
|
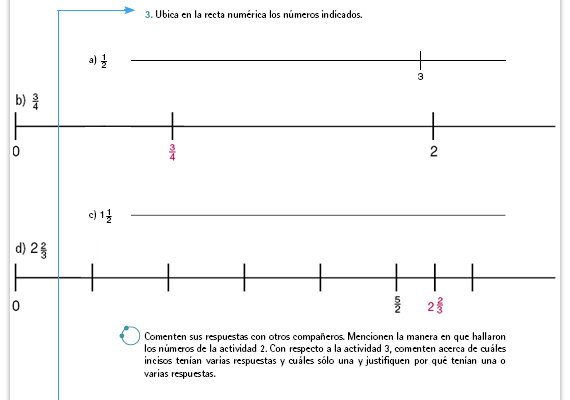
| Respuestas. En estos
problemas se combinan
rectas en las que no
está definida la escala y
rectas en las que ya está
definida.
En la recta del inciso a) solo hay un número como referencia (el 3), por lo tanto,  puede ubicarse
en cualquier punto a la
izquierda del 3. puede ubicarse
en cualquier punto a la
izquierda del 3.
En la recta del inciso b) no esta definida la escala. Es importante que los alumnos se den cuenta y que no traten de dividir el segmento del 0 al 2 en cuatro partes (pues cada una seria de tamano  y
no de y
no de 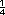 ). Si cometen este
error, pidales que localicen
primero el 1. ). Si cometen este
error, pidales que localicen
primero el 1.
En la recta del inciso c) no hay ninguna referencia, los alumnos deben colocar un número arbitrariamente (por ejemplo el 0) y luego ubicar 1 
En el inciso d) la respuesta es unica pues hay dos puntos de referencia. El número que debe hallarse (2 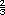 ) es mayor que el ) es mayor que el  (o
2 (o
2 ), por lo tanto estara a
su derecha. Para localizar
el punto exacto puede ser
util hallar el 3. Si dividen
el segmento de 0 a ), por lo tanto estara a
su derecha. Para localizar
el punto exacto puede ser
util hallar el 3. Si dividen
el segmento de 0 a  en
cinco pedazos iguales
(cada uno de tamano en
cinco pedazos iguales
(cada uno de tamano  )
podran ubicar los puntos
1 y 2. Anadiendo al )
podran ubicar los puntos
1 y 2. Anadiendo al  un
intervalo de tamano un
intervalo de tamano  tendran el 3 y solo resta
dividir el segmento del 2
al 3 en tercios.
tendran el 3 y solo resta
dividir el segmento del 2
al 3 en tercios.
|