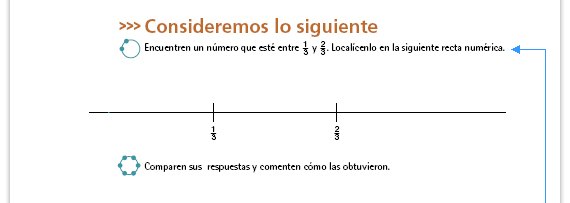
|

|

|
 |
 |

| Propósito de la sesión. Resolver
problemas de densidad de números
fraccionarios usando la recta
numérica como un recurso. Reconocer
la conservación de la escala y la
arbitrariedad de la posición del cero.
Organización del grupo. Casi todas las actividades se realizan en parejas y hay momentos de discusión grupal. La última actividad es individual. |

Posibles dificultades. Algunos alumnos pueden decir que entre 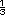 y y 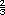 no
hay ningun número, pues no hay ningun
número (natural) entre 1 y 2. no
hay ningun número, pues no hay ningun
número (natural) entre 1 y 2.
Sugerencia didáctica. Permita que los alumnos trabajen por su cuenta en la actividad, no les proporcione información todavía. Para resolver las dificultades planteadas por el problema de la densidad, se propone que los alumnos recurran a la equivalencia de fracciones, que es un conocimiento que los alumnos trabajaron durante la escuela primaria. |

 Sugerencia didáctica. La densidad es
una propiedad que los números enteros
no poseen, y aunque en la primaria los
alumnos han trabajado con decimales
y fracciones, pueden tener dificultades
para hallar una fracción entre otras
dos. Por eso es importante que realicen
todas las actividades y que las comenten
grupalmente.
Sugerencia didáctica. La densidad es
una propiedad que los números enteros
no poseen, y aunque en la primaria los
alumnos han trabajado con decimales
y fracciones, pueden tener dificultades
para hallar una fracción entre otras
dos. Por eso es importante que realicen
todas las actividades y que las comenten
grupalmente. |

| Sugerencia didáctica. Comente esta
información con los alumnos.
También puede anotar las siguientes
parejas de números en el pizarrón y
pedirles que digan si hay al menos un
número que esté entre esos dos. Si
piensan que sí, que propongan alguno(s)
y que digan si es fraccionario, decimal o
natural.
5 y 6. Si entre estos dos números piensan que no existe al menos otro número, escríbalos como  y y 
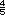 y y 
Pregunte tambien si entre ellos estaran el 1 y el 
1 y 1 
Para recordar. Los números naturales son los enteros positivos (no tienen parte fraccionaria o decimal ni son números negativos). Por ejemplo el 5, 81, 9 234, etcétera. |
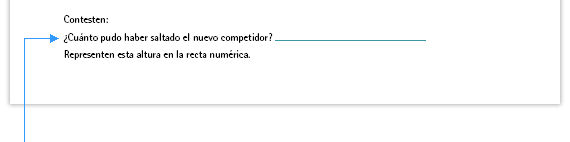
| Propósito de la pregunta. Al generar distintas fracciones equivalentes los alumnos podrán percatarse de que entre dos números fraccionarios existen varios más (en realidad, hay una infinidad de números). |

| Sugerencia didáctica. Si en este punto de la sesión hay alumnos que consideran que no existe otro número entre dos fracciones, permita que continúen trabajando, más adelante podrán aclararlo. |

| Propósito del interactivo. Comprobar la propiedad de densidad de los números fraccionarios. |

Respuestas.
|

| Propósito del interactivo. Comprobar la propiedad de densidad de los números fraccionarios. | Posibles procedimientos
|

Respuestas. Se puede esperar que de
inmediato los alumnos ubiquen el 1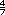 .
Para hallar otros dos números que esten entre 1 .
Para hallar otros dos números que esten entre 1 y 1 y 1  hay una infinidad de
respuestas posibles. Por ejemplo, pueden observar que: 1 hay una infinidad de
respuestas posibles. Por ejemplo, pueden observar que: 1 =
= 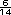 y que 1
y que 1 = 1 = 1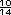 Entre ellos pueden ubicarse el 1
Entre ellos pueden ubicarse el 1 , 1 , 1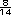 = 1
= 1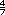 y 1 y 1
También sucede que: 1  = 1 = 1 = 1 = 1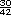
Entre ellos pueden ubicarse, por ejemplo, el 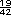 , ,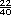 , ,
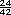 ,
, 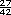 , , 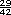 , etcetera.
Si considera que aún tienen dificultades con el concepto de densidad, realicen
mas ejercicios de este tipo. , etcetera.
Si considera que aún tienen dificultades con el concepto de densidad, realicen
mas ejercicios de este tipo.
Integrar al portafolios. Pida a los alumnos que resuelvan y copien en una hoja aparte esta actividad. Si considera que aun tienen dificultades para ubicar números entre dos fracciones, resuelvan colectivamente actividades de este tipo en el pizarron, resaltando la equivalencia, es decir, señalando en la recta que 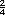 se localiza en el mismo punto que
se localiza en el mismo punto que  y que lo mismo ocurre con y que lo mismo ocurre con
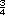 y
y 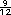 . Por eso
entre . Por eso
entre 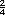 y y 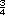 estan estan
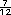 y
y 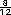 , entre otros. , entre otros. |
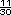
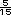 =
= 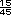
 y 2
y 2
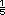 ).
Entonces pueden dividir
cada segmento en 2 y
hallar
).
Entonces pueden dividir
cada segmento en 2 y
hallar 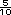 , encuentran las fracciones
equivalentes a
, encuentran las fracciones
equivalentes a  y a
y a 
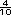
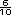
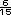 =
= 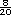
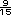 =
=