Propósito de la sesión. Resolver problemas de comparación y densidad de números decimales usando la recta numérica como un recurso. Reconocer la conservación de la escala y la arbitrariedad de la posición del cero. Organización del grupo. Se sugiere que los alumnos resuelvan todas las actividades organizados en parejas, a excepción de Lo que aprendimos, que se recomienda resolver de manera individual.

Posibles dificultades. Al ordenar las longitudes saltadas, uno de los errores que pueden surgir consiste en decir que 8.59 metros es mayor que 8.9 metros, "porque 59 es mayor que 9". En este punto no los corrija, el error se confrontará en la fase siguiente.

Sugerencia didáctica. Es muy importante permitir que los alumnos hagan comentarios sobre ideas, sus respuestas, sus intentos de resolución, etcétera, aunque estén equivocados. Escuchar lo que dicen los otros puede ser de utilidad para todos.

Propósito del interactivo. Comprobar la propiedad de densidad de los números decimales.

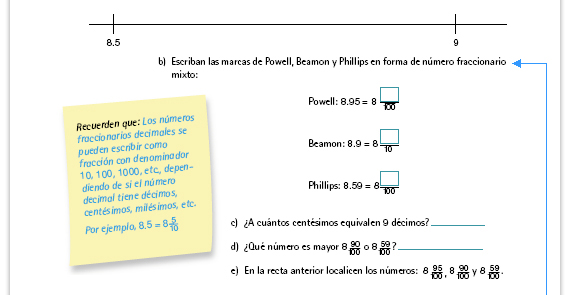
Propósito de la actividad. Para solucionar el posible error descrito antes, se recurre a la escritura fraccionaria de los números decimales y a la equivalencia de fracciones.

Sugerencia didáctica. Si hubo errores en la sección Consideremos lo siguiente corríjalos en este momento.

Propósito de la actividad. En esta actividad se aborda el problema de la densidad de los números decimales. En este caso, entre 8.90 y 8.95 se pueden localizar cuatro números en el orden de los centésimos: 8.91, 8.92, 8.93, 8.94. Para encontrar la quinta marca hay que considerar los milésimos. La idea es que los alumnos vayan comprendiendo que entre dos números decimales o fraccionarios hay una infinidad de números. Por ejemplo, entre 8.91 y 8.92 pueden estar 8.915 y 8.916, y entre estos 8.9152 y 8.9153, etcétera.

Respuestas. b) 8.915 Posibles dificultades. Para algunos alumnos puede no ser muy claro que 8.905 esté entre 8.90 y 8.91 porque en su experiencia con los números naturales 905 es mayor que 90 y que 91. Si esto sucede, puede resultarles útil hallar un número equivalente: 8.90 = 8.900 8.91 = 8.910 Así podría ser más claro que 8.905 está a la mitad entre esos dos números.

Sugerencia didáctica. Comente esta información con los alumnos. También puede anotar las siguientes parejas de números en el pizarrón y pedirles que digan si hay al menos un número que esté entre esos dos. Si piensan que sí, que propongan alguno(s) y que digan si es fraccionario, decimal o natural. 0.36 y 0.37 2.456 y 2.457

Respuestas. Es conveniente situar primero las unidades (1 y el 2). El 0.5 se ubica a mitad entre el cero y el uno. Para ubicar 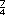, los alumnos pueden transformarlo en número decimal, obteniendo 1.75, despues pueden dividir el segmento entre el 1 y el 2 en diez partes iguales y ubicar 0.75 entre 7 decimos y 8 decimos. Si trabajan con la fracción, requieren dividir el segmento entre el 1 y el 2 cuatro partes iguales para ubicar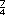

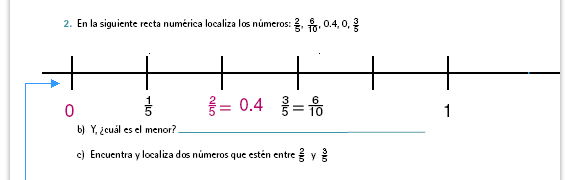
Posibles procedimientos. Aun cuando no se esta marcando el 0, los alumnos pueden identificar que entre 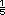y 1 hay cuatro quintos, que son los que deberan marcar. Una vez obtenido el tamano de 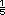pueden hallar el 0 Para ubicar a cada uno de los números que se les indican, los alumnos tienen la opcion de transformar algunos de ellos a fracciones o a números decimales, o pueden obtener tambien fracciones equivalentes; por ejempl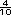o, = ó 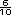= Integrar al portafolios. Pida a los alumnos que resuelvan y copien en una hoja aparte los ejercicios del número 2 de esta sección. En ellos se abordan la localización de decimales y fracciones en la recta, la equivalencia y la densidad, por lo que puede ser un buen indicativo de los conocimientos de los alumnos. Si tienen dificultades resuelvan actividades como las de las secciones Manos a la obra de las sesiones 2 y 3. Sugerencia didáctica. Invite a los alumnos a que decidan con qué tipo de números quieren trabajar; posteriormente, cuando comparen sus soluciones, será interesante que identifiquen la diversidad de respuestas correctas. Respuestas. 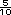a) y que son equivalentes b) el 0 c) Una forma de encontrar dos puntos entre y , es hallar números equivalentes: = y = ; entre esos dos números esta Posteriormente pueden obtenerse quinceavos: 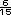= y y 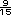; entre esos dos números estan 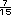y 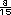. 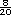Si se transforma a veinteavos, tenemos que entre y 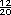se ubican 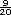, 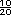y La pregunta admite una gran diversidad de respuestas correctas.