Propósito de la sesión. Describir las reglas de secuencias de figuras de manera verbal o aritmética. Organización del grupo. Forme parejas para que los alumnos trabajen de esa manera durante toda la sesión.

Eje

Sentido numérico y pensamiento algebraico.

Tema

Significado y uso de los números.

Antecedentes

Durante la escuela primaria los alumnos completaron sucesiones numéricas sencillas. En esta ocasión utilizarán sucesiones numéricas y figurativas para encontrar la expresión general que define un elemento cualquiera de la sucesión.

Propósitos de la secuencia Construir sucesiones de figuras y números a partir de una regla dada. Determinar expresiones generales que definen las reglas de sucesiones numéricas y figurativas.
Sesión	Título y propósitos de la sesión	Recursos
1	Figuras que crecen Describir las reglas de sucesiones de figuras de manera verbal o aritmética.	Video "Figuras que crecen" Interactivo
2	Números que crecen Describir la regla de crecimiento de sucesiones de números de manera verbal o aritmética.	Interactivo
3	Escribiendo reglas Determinar expresiones generales para definir las reglas de sucesiones de números o de figuras llamando "figura n" a la que ocupa el "lugar n".	Interactivo

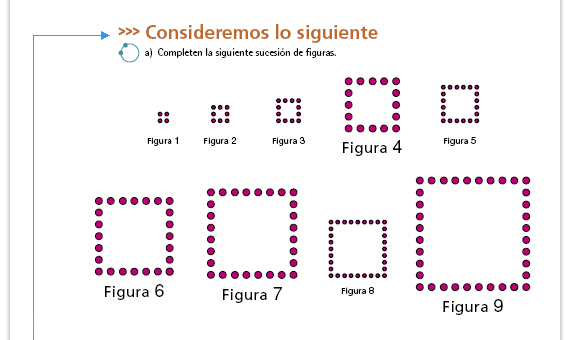
Propósito del video. Observar sucesiones de figuras y de números que crecen, para deducir su patrón de crecimiento.

Posibles procedimientos. Una manera en que los alumnos pueden resolver, el ejercicio es continuar dibujando cuadrados aumentando un punto a cada lado. Es poco probable que en este momento consideren el total de puntos de la figura o que establezcan una relación entre el lugar que ocupa la figura en la sucesión y el total de puntos que debe tener. Posibles dificultades. Como de la figura 1 a la figura 2 el número de puntos aumenta el doble, un posible error es que consideren que siempre deben aumentar el doble. Permita que resuelvan como puedan, más adelante tendrán oportunidad de comparar y corregir sus resultados. Respuestas. El número de puntos de cada figura aumenta de cuatro en cuatro: Fig. 4 = 16 puntos; Fig. 6 = 24 puntos; Fig. 7 = 28 puntos; Fig. 9 = 36 puntos.

Propósito del interactivo. Deducir reglas correspondientes a sucesiones numéricas y figurativas.

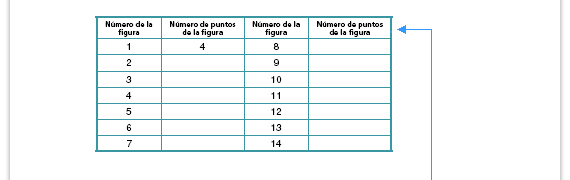
Propósito de la actividad. Identificar las relaciones entre el número de la figura y el número de puntos de la figura; al mismo tiempo, podrán comparar, y en su caso corregir, las respuestas que obtuvieron en un primer momento. Posibles procedimientos. Algunos alumnos pueden identificar que los valores de la segunda y cuarta columna aumentan de cuatro en cuatro; otros podrán ver que es posible obtenerlos al multiplicar el número de la figura por 4; también pueden notar que cada lado del cuadrado tiene un punto más que el número de la figura: la figura 1 es un cuadrado con dos puntos por lado, la figura 2 es un cuadrado con tres puntos por lado, etcétera. Mientras resuelven, pregúnteles cómo están completando la tabla.

Posibles procedimientosprocedimientos para resolver pueden ser diversos, así como la forma de expresarlos, por ejemplo: "Para la figura 14 son los puntos de la 13 más cuatro". "Le sumo 4". "El lugar de la figura por cuatro". "Como la figura 14 tiene 15 puntos por lado, multiplico 15 × 4 y le resto 4 puntos porque estoy contando dos veces las esquinas". Fomente el intercambio de ideas, incluyendo procedimientos correctos e incorrectos.

Respuesta. Los tres últimos procedimientos son correctos, aunque el penúltimo ("Son los múltiplos de 4") da una respuesta tan general que puede ser ambigua cuando se trata de establecer el número de puntos para una figura determinada; por ejemplo, ¿cuál de todos los múltiplos de 4 es el número de puntos para la figura 14?

Sugerencia didáctica. Pídales que utilicen uno de los procedimientos que consideren correctos para obtener el total de puntos de las figuras 15 y 20. Para que puedan compararse los resultados que se obtienen con cada procedimiento, asegúrese de que efectivamente cada uno de ellos sea utilizado al menos por una de las parejas (incluyendo el procedimiento incorrecto). Respuestas: La figura 15 tiene 60 puntos (15 × 4) y la figura 20 tiene 80 puntos (20 × 4).

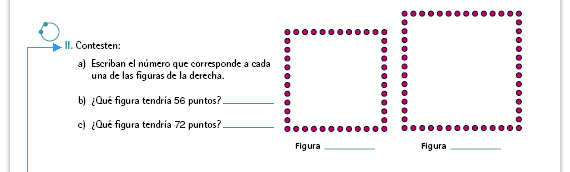
Respuestas a) Figura 11 y figura 13, respectivamente. Pueden contar el número total de puntos y dividirlo entre cuatro; también pueden contar el número de puntos por lado y restar uno. b) La figura que tiene 56 puntos es la número 14. c) La figura que tiene 72 puntos es la número 18.

Respuestas. Las respuestas pueden ser diversas, desde aquellas que no identifiquen una razón ("Por que no hay", "Porque así van saliendo") hasta otras en las que haya una justificación matemática: " Porque todos los múltiplos de 4 son pares".

Sugerencia didáctica. Lea y comente esta información junto con los alumnos. Una forma de recuperar la información es que usted les pida que averigüen el número de puntos para una figura dada (por ejemplo, para la figura número 19) utilizando las tres reglas que se dan en el recuadro. Si obtienen los mismos resultados, los alumnos podrán verificar que, efectivamente, las tres reglas son equivalentes.

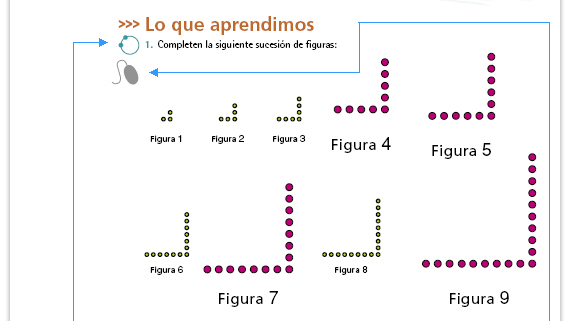
Posibles procedimientos. Al contar el número de puntos de las tres primeras figuras, es posible que los alumnos identifiquen que aumentan dos puntos de una figura a otra. Para dibujar las figuras, deberán aumentar un punto en cada uno de los extremos. Respuestas. La figura 4 tiene nueve puntos, la figura 5 tiene once puntos, la figura 7 tiene quince puntos y la figura 9 tiene diecinueve puntos.

Propósito del interactivo. Deducir reglas correspondientes a sucesiones numéricas y figurativas.

Sugerencia didáctica. Para que los alumnos puedan elegir alguna o algunas de las reglas, pídales que anoten, debajo de cada figura, el número de puntos de cada una de ellas. Respuesta. Sólo la primera y la tercera reglas son equivalentes; invite a los alumnos a argumentar sus respuestas. Es posible que la segunda regla ("Los números impares") genere polémica, pues si bien en todos los casos el número total de puntos es un número impar, en la sucesión no hay una figura que tenga sólo un punto; por lo tanto, esa regla no es correcta.

Recuerde que. En esta actividad se presentan dos tipos de reglas: una regla recursiva y una regla expresada como una fórmula. En las reglas recursivas el valor de cada término depende de algunos de los términos anteriores de la sucesión; en este caso depende únicamente del valor del término anterior. Esta es la característica de la primera regla ("El número de puntos de la figura anterior más dos puntos"); los alumnos que la utilicen tendrán que calcular el número de puntos para las figuras 6 y 7 para poder obtener el número de puntos de la figura 8 que se les pide en la tabla. En las reglas expresadas como una fórmula, el valor de cada término depende únicamente del mismo término; es el caso de la tercera regla ("Multiplicar por dos el número de la figura y sumar uno"): no se requiere conocer el número de puntos de la figura anterior y se obtiene, de manera inmediata, el número de puntos de cualquier figura. Es conveniente que los alumnos vayan identificando algunas ventajas y desventajas de cada una de las reglas; esto no quiere decir que usted deba enseñarles los términos "regla recursiva" o "regla expresada como una fórmula", sino únicamente que los alumnos identifiquen las diferencias y ventajas de cada una de las reglas que se les proponen.

Respuestas. Figuras 25 y 30, respectivamente. No puede haber una figura con 62 puntos porque el total de puntos de todas las figuras es un número impar.

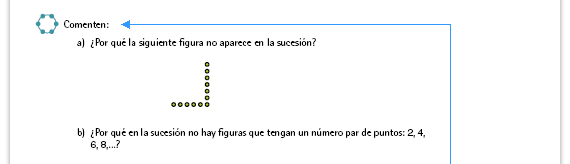
Respuesta. No hay figuras con un número par de puntos porque el número de puntos de una figura es dos veces el número de la figura más 1, lo que resulta siempre un número impar.