Propósito de la sesión. Que los alumnos logren determinar expresiones generales para definir las reglas de secuencias de números o de figuras, llamando "figura n" a la que ocupa el "lugar n". Organización del grupo. Se sugiere que los alumnos trabajen organizados en parejas, a excepción del apartado Lo que aprendimos, el cual puede resolverse de manera individual.

Respuestas. Los términos van aumentando de 7 en 7, por lo tanto, hay que multiplicar el lugar del término por 7 para encontrar el término que corresponde.

Respuestas. Hay varias formas correctas de expresar la regla: n × 7, 7 por n, 7 veces n.

Sugerencia didáctica. Pida a las parejas que compartan con el grupo cómo entendieron la expresión lugar n. Es importante dejar claro que lugar n se refiere a "cualquier lugar"; la regla que cada pareja haya redactado debe permitir encontrar, efectivamente, el término para cualquier lugar. Permita que los alumnos valoren qué reglas cumplen con esa condición; en caso de que no todas las parejas hayan redactado una regla correcta, posteriormente tendrán oportunidad de identificar su error.

Respuestas. Cada uno de los términos de esta columna se obtiene multiplicando por 7 el lugar del término.

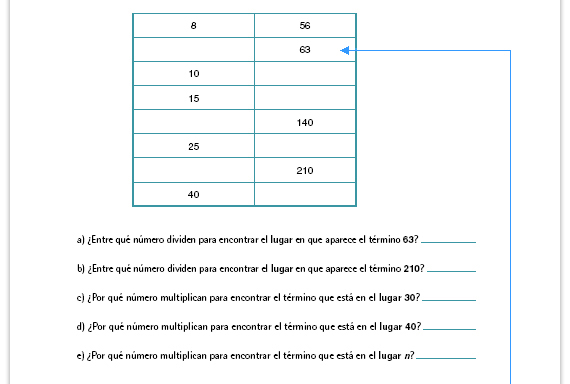
Respuesta. El lugar del término se obtiene dividiendo el término entre siete: 63 ÷ 7 = 9.

Respuesta. La cuarta regla (Multiplicar n por 7) es la que permite encontrar el término n por la precisión del lenguaje que utiliza. Sugerencia didáctica. Es importante que los alumnos argumenten por qué eligieron determinadas reglas. Posteriormente, usted puede aclarar que en la segunda y la tercera regla (que probablemente algunos alumnos eligirán) el lenguaje no es preciso (¿qué es lo que hay que multiplicar por 7?, ¿cuál es el término anterior al que debemos sumar 7?); además, la tercera regla da lugar a distintas sucesiones si decidimos cambiar el primer término. Por ejemplo: una sucesión puede iniciar con el número 7 (7, 14, 21...) y otra puede iniciar con el 5 (5, 12, 19...), en ambas sucesiones se suma 7 al término anterior. Una vez que hayan identificado la regla correcta, invítelos a compararla con la que ellos redactaron en el inciso e del apartado Consideremos lo siguiente y que hagan las correcciones necesarias.

Respuestas. Para los incisos a, b y c, se multiplica el lugar por 7; para el inciso d se divide el término entre 7.

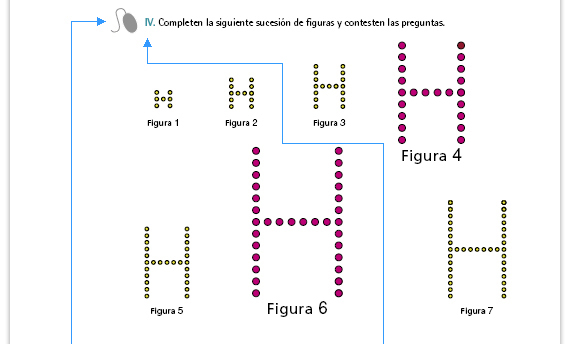
Propósito del interactivo. Deducir reglas correspondientes a sucesiones numéricas y figurativas.

Posibles dificultades. Si observa que algunos alumnos no encuentran ninguna estrategia para abordar el problema, puede sugerirles que escriban debajo de cada figura el número de puntos que le corresponde; de esta manera podrán identificar más fácilmente que el número de puntos aumenta de cinco en cinco de una figura a otra: un punto en cada uno de los cuatro extremos y otro en medio. Es importante que les dé la oportunidad de tratar de resolverla, aun cuando no lo hagan de manera correcta.

Respuestas. Figura 4: 22 puntos; Figura 7: 37 puntos; Figura 9: 47 puntos; Figura 10: 52 puntos.

Respuestas. Las tres reglas son correctas y equivalentes. No obstante, la primera regla no permite obtener de manera directa el número de puntos para cualquier término, pues se requiere calcular primero el número de puntos del término anterior.

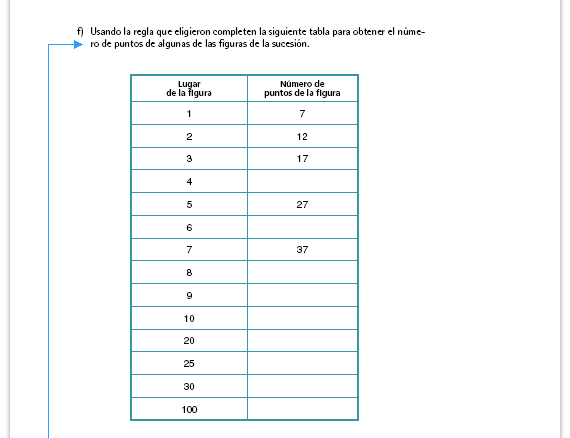
Sugerencia didáctica. Antes de que los alumnos completen la tabla utilizando la regla que eligieron, usted puede solicitarles que argumenten por qué consideran que esa regla es la que más les convence. Particularmente será necesario que expresen cómo interpretan la regla 5n + 2.

Sugerencia didáctica. Como una forma de recuperar la información usted puede proponer al grupo algunas reglas en el pizarrón, por ejemplo: 5n o 3n, y pedir a los alumnos que traten de interpretarlas para el término que está en primer lugar, para el que está en segundo, etcétera.

Propósito del interactivo. Deducir reglas correspondientes a sucesiones numéricas y figurativas.

Integrar al portafolios. Se espera que los alumnos sean capaces de identificar la regla de la sucesión y que puedan formularla mediante una expresión general. Si nota que tienen dificultad para identificar la regla, sugiérales que realicen una tabla como la de la actividad III de Manos a la obra. Si tienen dificultades para formular la expresión general, revise y comente nuevamente, junto con los alumnos, la información del recuadro A lo que llegamos. Procure hacer un análisis similar con algunas de las reglas que los alumnos hayan generado para este ejercicio, y ayúdeles a identificar las reglas equivalentes y a expresarlas utilizando la letra n.

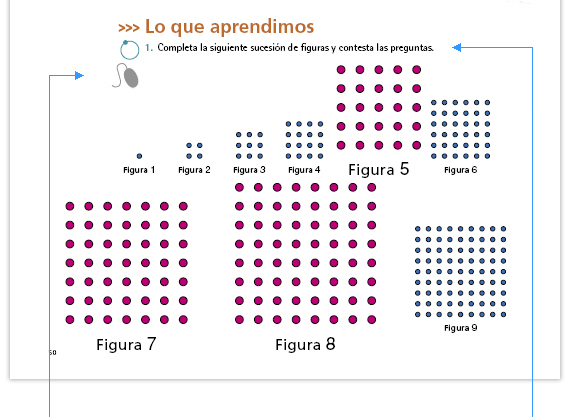
Respuestas. El número de puntos de cada figura,es igual al cuadrado del lugar de la figura: la figura 5 tiene 25 puntos (5 x 5), la figura 7 tiene 49 puntos (7 x 7), la figura 8 tiene 64 puntos (8 x 8).

Respuestas. a) La figura 5. b) 64 puntos. c) La figura 10. d) 400 puntos. e) Algunas respuestas correctas son: n x n , n por n, n2