Propósito de la sesión. Elaborar expresiones algebraicas para calcular el perímetro de cuadrados, rectángulos, polígonos regulares y otras figuras. Operar con literales. Organización del grupo. Se recomienda que los alumnos trabajen en parejas, y que el apartado Lo que aprendimos se resuelva de manera individual.

Eje

Sentido numérico y pensamiento algebraico.

Tema

Significado y uso de los números.

Antecedentes

En la escuela primaria los alumnos resolvieron situaciones en las que debían interpretar o construir fórmulas geométricas para calcular el perímetro y el área de algunas figuras. En esas situaciones las literales que utilizaron eran interpretadas como etiquetas o abreviaturas. En esta ocasión se retomarán ese tipo de situaciones para interpretar las literales como números generales con los que se puede hacer operaciones.

Propósitos de la secuencia Explicar en lenguaje natural el significado de algunas fórmulas geométricas, interpretando las literales como números generales con los que es posible operar.
Sesión	Propósitos de la sesión	Recursos
1	Fórmulas y perímetros. Elaborar expresiones algebraicas para calcular el perímetro de cuadrados, rectángulos, polígonos regulares y otras figuras. Operar con literales.	Video "Fórmulas y perímetros" Interactivo
2	Fórmulas y áreas. Elaborar expresiones algebraicas para calcular las áreas de las figuras anteriores.	Interactivo

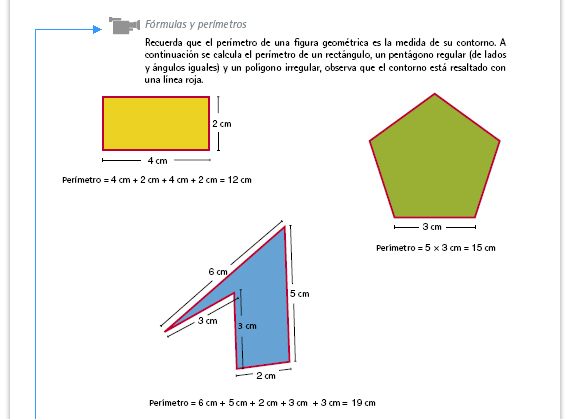
Propósitos del video. Reconocer el perímetro como el contorno de una figura y calcularlo en algunos polígonos.

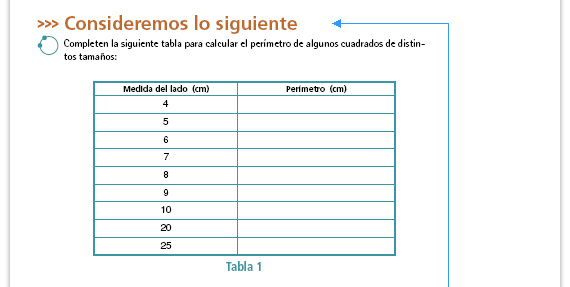
Propósito de la actividad. Se espera que los alumnos calculen los perímetros sin mayores dificultades, (pueden multiplicar la medida del lado por 4 o sumar cuatro veces la medida del lado). La finalidad está centrada en que logren verbalizar cuál es el procedimiento que utilizaron para obtener el perímetro en todos los casos (inciso a), y que posteriormente traten de generalizar ese procedimiento utilizando una literal (inciso b).

Respuestas. Hay distintas formas de responder, lo importante es que los alumnos traten de expresar o verbalizar el procedimiento que utilizaron para completar la tabla. Algunas respuestas posibles son: "Multiplicando la medida del lado por 4", "Sumando cuatro veces el lado", "L × 4".

Propósito del interactivo. Deducir las expresiones algebraicas de fórmulas de áreas y perímetros.

Posibles errores. En los casos anteriores los alumnos sumaron medidas expresadas con números, pero en este caso se trata de sumar o de multiplicar una literal que también representa una medida. Es posible que este cambio en la representación de medidas les dificulte responder a la pregunta o que lo hagan de manera errónea (por ejemplo, podrían contestar x + 4 o utilizar algunas otras expresiones sin sentido). No se preocupe si en este momento no pueden responder de manera correcta, en el siguiente apartado tendrán oportunidad de ver distintas formas de generalizar. Algunas respuestas correctas: 4 x, 4 por x, 4 veces x, x + x + x + x.

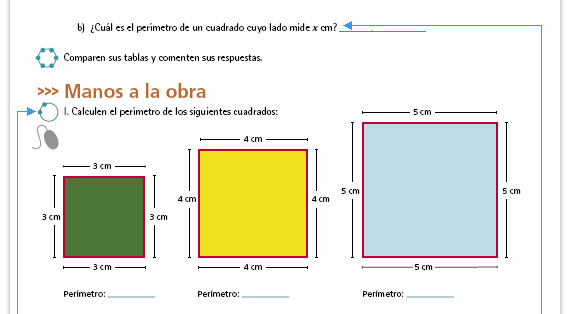
Propósito de la actividad. Por una parte, se espera que los alumnos verbalicen el procedimiento que utilizaron para calcular el perímetro de los cuadrados, y por la otra, que la expresión (verbal o simbólica) de ese procedimiento sea tan general que permita obtener el perímetro de cualquier cuadrado. Las respuestas pueden ser diversas: "Sumando cuatro veces la medida del lado", "Multiplicando por cuatro la medida del lado", L × 4, L + L + L + L.

Respuesta. Las cuatro últimas expresiones son correctas.

Sugerencia didáctica. Pida a los alumnos que argumenten por qué cada una de las expresiones —o reglas— es válida o no. Una forma de verificar sus respuestas es calculando el perímetro del cuadrado de 30 cm que se sugiere. Una vez que hayan acordado cuáles son las expresiones correctas, pueden comentarse ventajas o desventajas de algunas de esas expresiones; por ejemplo, en la segunda, puede confundirse la "x" con el símbolo de multiplicación.

Sugerencia didáctica. En la sesión 1 de la secuencia 3 los alumnos identificaron reglas equivalentes, por lo que usted puede retomar lo que ellos ya saben al respecto para poder interpretar la información que ahora se les presenta sobre las expresiones equivalentes.

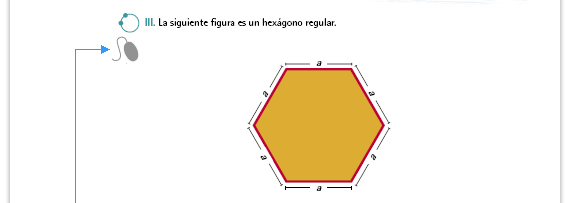
Propósito del interactivo. Deducir las expresiones algebraicas de fórmulas de áreas y perímetros.

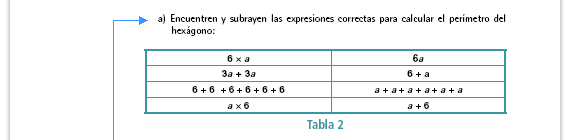
Respuestas. Las expresiones correctas son: 6 × a, 3a + 3a, a × 6, 6a, a + a + a + a + a + a.

Propósito de la actividad. Al aplicar a casos específicos las expresiones que los alumnos eligieron, tendrán la oportunidad de verificar si efectivamente las distintas expresiones son equivalentes o no. Sugerencia didáctica. Es conveniente que una vez identificadas las expresiones correctas, los alumnos comenten las ventajas y desventajas de algunas de ellas, particularmente la confusión que podría provocar el uso del símbolo de multiplicación "×", pues se puede confundir con la letra "x". También es importante enfatizar que la expresión 6a puede interpretarse como 6 por a o 6 veces a.

Sugerencia didáctica. Una vez que hayan leído y comentado la información que aquí se presenta, pueden acordar en el grupo utilizar en adelante expresiones como la de 6a para sustituir el signo de multiplicación "x" y evitar así posibles confusiones.

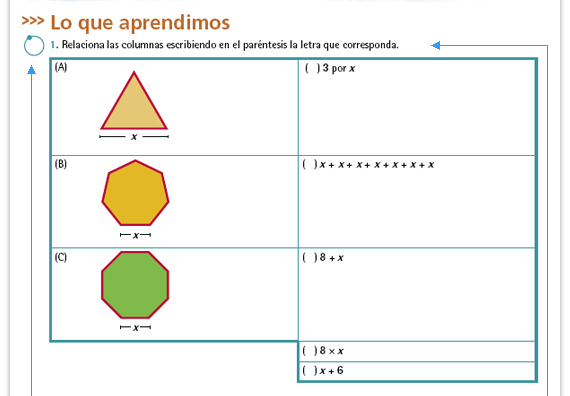
Propósito de las actividades. Al inicio de esta sesión se plantearon situaciones en las que las medidas se dieron con números para que a partir del cálculo aritmético los alumnos pudieran verbalizar y generalizar sus procedimientos; en las situaciones que a continuación se plantean, se espera que los alumnos logren expresar relaciones utilizando únicamente literales.

Respuestas. (A) 3 por x (B) 8 × x (C) x + x + x + x + x + x + x

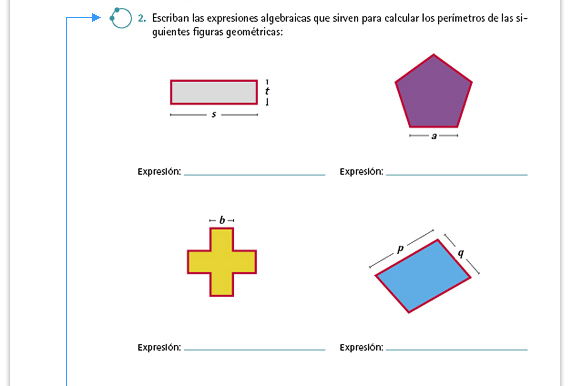
Respuestas. Algunas posibles, son: Para el rectángulo: s + s + t + t, y también 2s + 2t. Para el pentágono: 5a, y también a +a + a + a + a. Para 12b el dodecágono (la cruz): 12m. Para el romboide: 2p + 2q, y también p + p + q + q.