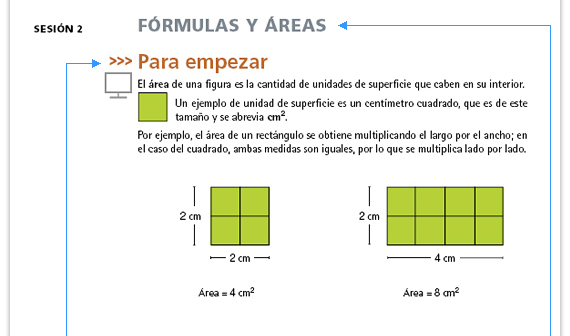
Sugerencia didáctica. Durante la escuela primaria los alumnos trabajaron ampliamente el cálculo de áreas de diversas figuras geométricas utilizando distintos recursos, por lo que se espera que no tengan dificultades relevantes. No obstante, es recomendable que esta información se lea y se comente con todo el grupo con la finalidad de que la noción de área no sea una dificultad para resolver los problemas que se plantean en esta sesión.

Propósito de la sesión. Elaborar expresiones algebraicas para calcular áreas de las figuras anteriores. Organización del grupo. Se sugiere que los alumnos trabajen en parejas, a excepción del apartado Lo que aprendimos, el cual se recomienda trabajar de manera individual.

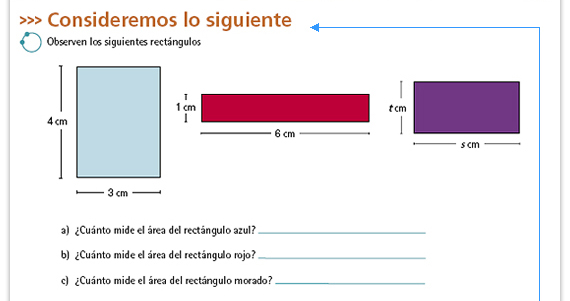
Posibles procedimientos. Para el primero y el segundo rectángulo se espera que los alumnos multipliquen el largo por el ancho, aunque también podrían cuadricular la superficie en unidades cuadradas y contarlas, como se muestra en el ejemplo del apartado Para empezar; en cambio, para el tercer cuadrado los alumnos tendrán que recurrir a una expresión algebraica, por ejemplo: t por s, ts. Es posible que tengan dificultades para este último caso, o que se confundan con la regla para calcular el perímetro.

Sugerencia didáctica. Invite a los alumnos a que expliquen cómo obtuvieron sus resultados, sobre todo para el caso del tercer rectángulo. Aquí es particularmente interesante que identifiquen cuáles expresiones son equivalentes.

Propósito del interactivo. Deducir las expresiones algebraicas de fórmulas de áreas y perímetros.

Propósito de la actividad. Se espera que al completar la tabla los alumnos identifiquen —o constaten— que para obtener el área de cualquier rectángulo se multiplica el largo por el ancho. Sugerencia didáctica. Dibuje la tabla en el pizarrón para que una vez que los alumnos la hayan completado, algunos de ellos pasen al pizarrón a escribir sus respuestas y puedan compararlas.

Respuestas. Las expresiones correctas son la tercera, la cuarta y la sexta.

Anime a los alumnos a que argumenten por qué consideran que las expresiones que eligieron son las correctas, y por qué consideran que las otras no lo son. Una forma de verificar sus respuestas es calculando el área de las figuras que se sugieren utilizando las reglas elegidas; de esa misma forma pueden identificar qué expresiones son equivalentes.

Sugerencia didáctica. Comente con los alumnos que las expresiones ts y t × s también son equivalentes.

Respuestas. b × b, y bb.

Sugerencia didáctica. Copie la tabla en el pizarrón y pida a algunas parejas que escriban en ella sus resultados. En caso de que haya resultados diferentes, pida al grupo que revise las expresiones que se utilizaron y que identifique aquellas que son equivalentes y correctas (4 × b, 4b, y b + b + b + b son equivalentes entre sí, pero no permiten calcular el área del cuadrado).

Integrar al portafolios. Se espera que los alumnos logren expresar de manera algebraica el procedimiento para calcular el área de un triángulo. Si nota alguna dificultad, retome algunas de las expresiones correctas y otras incorrectas que hayan surgido de los mismos alumnos, y pídales que calculen el área de los triángulos que se sugieren en el inciso b. Posteriormente, analice junto con ellos qué expresiones son correctas y equivalentes, y cuáles no son correctas. Respuesta: Puede haber varias expresiones correctas: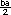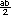