Propósito de la sesión. Explicitar que los puntos simétricos están a la misma distancia del eje de simetría y que el segmento que los une es perpendicular al eje de simetría. Materiales. Escuadras, regla, transportador y compás para los alumnos; de ser posible, un juego de geometría grande para el maestro. Organización del grupo. Aun cuando en la sesión hay momentos de trabajo individual, en equipos y de intercambio grupal, usted puede organizar equipos desde el inicio y mantenerlos durante para toda la sesión.

Eje

Forma, espacio y medida.

Tema

Transformaciones.

Antecedentes

En la escuela primaria los alumnos trabajaron con situaciones que ponen en juego la noción de simetría con respecto a un eje (simetría axial): aprendieron a identificar ejes de simetría y a distinguir figuras simétricas de las que no lo son; asimismo, trabajaron con la medición de ángulos, el trazo de rectas paralelas y perpendiculares y la medición de la distancia de un punto a una recta, aspectos vinculados a las propiedades de la simetría que se estudiarán en esta secuencia.

Propósitos de la secuencia Construir figuras simétricas respecto a un eje, analizarlas y explicitar las propiedades que se conservan en figuras tales como: triángulos isósceles y equiláteros, rombos, cuadrados y rectángulos.
Sesión	Propósitos de la sesión	Recursos
1	Como si fuera un espejo Explicitar que los puntos simétricos están a la misma distancia del eje de simetría y que el segmento que los une es perpendicular al eje de simetría.	Interactivo
2	Papel picado Trazar figuras simétricas con respecto a un eje utilizando sus instrumentos geométricos.	Interactivo
3	Los vitrales Explicitar las propiedades que se conservan en figuras simétricas: igualdad de lados y ángulos, paralelismo y perpendicularidad de lados.	Video "Vitrales"
4	Algo más sobre simetría Practicar los conocimientos adquiridos al resolver diversos ejercicios.

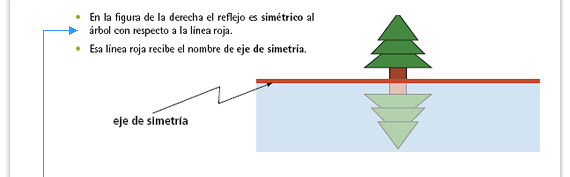
Recuerde que. La simetría axial es una propiedad de las figuras: una figura es simétrica con respecto a un eje cuando se traza una recta que divide en dos a la figura, de manera que la recta sirve como espejo: lo que se ve de un lado está también del otro, pero con la orientación contraria. La simetría con respecto a un eje es uno de los movimientos rígidos en el plano, caracterizados porque no cambian el tamaño ni la forma.

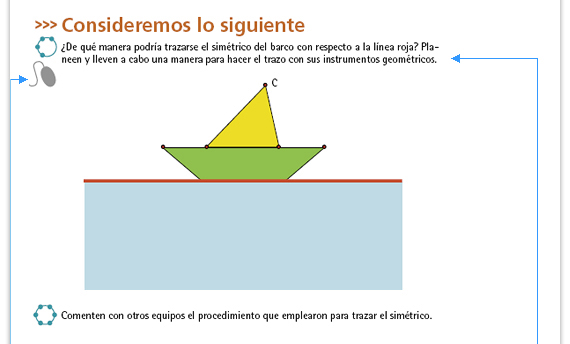
Posibles procedimientos. Algo que podrían hacer de manera inmediata es calcar el barco y reproducirlo simétricamente en la parte azul; otros podrían medir, aunque es probable que tomen las medidas con respecto al eje de manera imprecisa, esto es, sin trazar perpendiculares y haciendo uso de la regla en lugar del compás -que es más preciso para trasladar medidas-. Puede suceder que en lugar de reflejar el barco lo trasladen, esto es, que tracen la figura sin cambiar su orientación. No los corrija en este momento, a lo largo de la sesión tendrán oportunidad de notar por sí mismos su error. Permita que resuelvan sin darles pistas, tampoco es necesario que resuelvan un problema similar antes de trabajar esta lección. Motívelos a que realmente discutan las posibles maneras de solucionarlo e invítelos a utilizar sus instrumentos geométricos. Respuesta: El trazo correcto se muestra en la actividad II del apartado Manos a la obra.

Propósitos del interactivo. Que los alumnos desarrollen la idea de simetría de puntos de manera intuitiva y que descubran y utilicen las dos propiedades de los puntos simétricos.

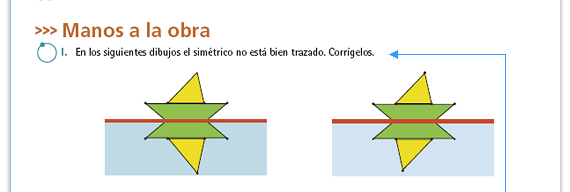
Propósito de la actividad. Se espera que los alumnos empiecen a notar que las figuras simétricas deben cumplir ciertas condiciones. En el primer caso el punto C y su simétrico no equidistan (no guardan la misma distancia) con el eje; en el segundo caso, a pesar de que el punto C y su simétrico sí equidistan del eje, si los unimos el segmento no es perpendicular al eje de simetría.

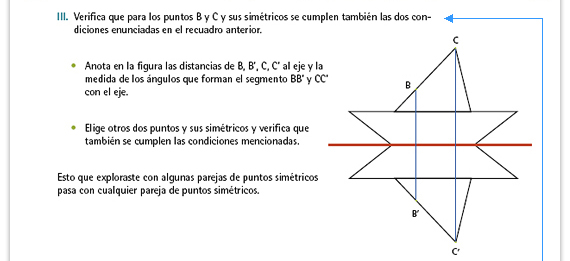
Posibles dificultades. Los alumnos aprendieron en la primaria a medir distancias de un punto a una recta (por ejemplo, las alturas de los triángulos), sin embargo es probable que cometan el error de medir la distancia utilizando otra recta en lugar de la perpendicular. Si nota que son varios los que tienen dificultades, usted puede mostrar al grupo la manera de hacerlo. Respuestas. La medida para el inciso a y la medida para el inciso b deben ser las mismas. La medida del ángulo debe ser de 90°.

Sugerencia didáctica. Si lo considera necesario, recuerde al grupo: 1)Cómo se usa el transportador para medir ángulos. 2)Que las rectas que forman ángulos de 90º se llaman perpendiculares. Recuerde que. Para medir ángulos es necesario que el vértice del ángulo coincida con la marca del transportador:

Sugerencia didáctica. Cerciórese de que los alumnos realmente lleven a cabo esta actividad en el trazo del problema inicial.

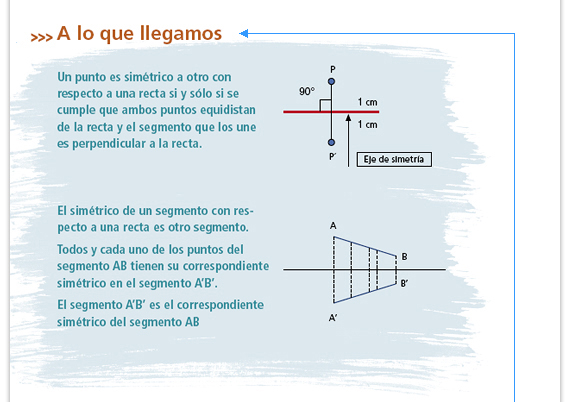
En las clases de matemáticas es sumamente importante establecer un concepto o un procedimiento; comente con el grupo la información del recuadro, y si lo considera conveniente, pida que la copien en su cuaderno. Sugerencia didáctica. Haga énfasis en que el primer párrafo del recuadro se refiere a un punto; en cambio, en el segundo párrafo se generaliza para todos los puntos de un segmento.