Propósito de la sesión. Explicitar las propiedades que se conservan en figuras simétricas: igualdad de lados y ángulos, paralelismo y Organización del grupo: Forme parejas para resolver el problema inicial; el resto de la sesión puede trabajarse de manera individual con momentos de intercambio entre todo el grupo. Materiales. Juego de geometría.

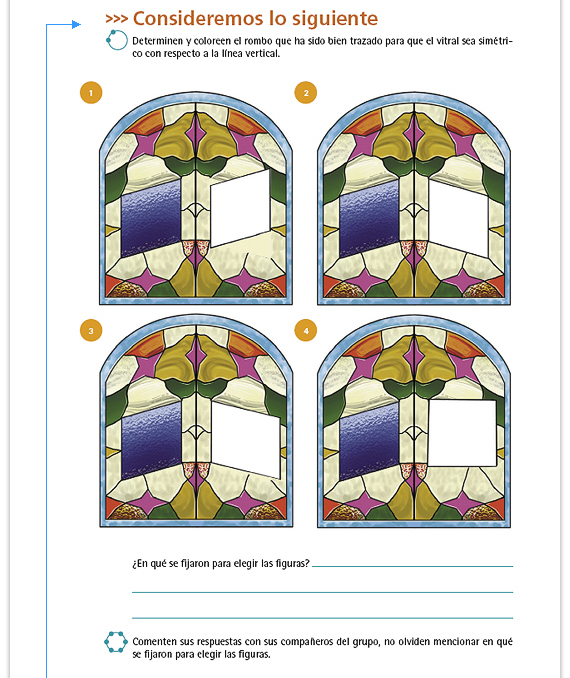
Sugerencia didáctica. Los alumnos saben, intuitivamente, que las figuras simétricas son del mismo tamaño. Se espera que usen esa idea para resolver este problema; no obstante, se han puesto figuras de tamaño muy similar para, de alguna manera, obligarlos a medir. Si nota que los alumnos contestan sin recurrir a la medición, puede plantearles la pregunta: "¿Cómo pueden asegurarse de que la figura elegida es la correcta?". Respuesta. En el primer vitral ambos rombos son iguales, pero la orientación del segundo de ellos no corresponde al reflejo del otro. En el tercer vitral la medida de los ángulos es igual, pero no la medida de los lados. En el cuarto vitral lo que cambia es la medida de los ángulos. El único vitral correcto es el segundo.

Propósito de las actividades. Las actividades del apartado Manos a la obra pretenden, por una parte, que aquellos alumnos que no se fijaron en la medida de los lados y los ángulos se den cuenta de que es necesario considerar ambas medidas; y por otra parte, que además de la igualdad de la medida de ángulos y de lados, observen que la distancia de un punto al eje debe ser la misma que la de su simétrico, formando una recta perpendicular con respecto al eje.

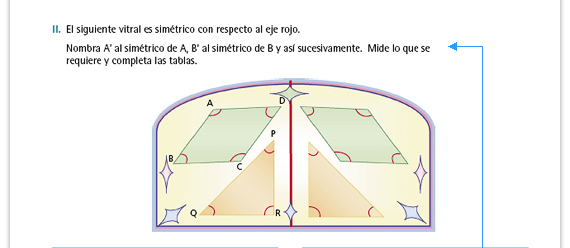
Respuestas. La medida de cada uno de los segmentos debe ser igual a la medida de su simétrico. De la misma manera, la medida de cada uno de los ángulos interiores debe ser igual a la medida del ángulo del vértice que le corresponde en su simétrico.

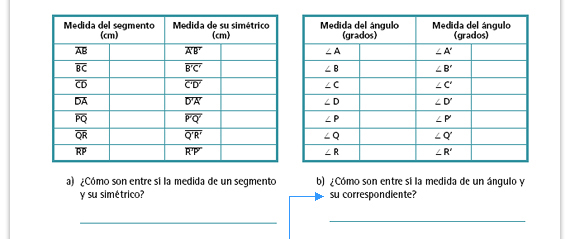
Sugerencia didáctica. Generalmente, los alumnos saben más de lo que expresan, sin embargo, es probable que ante este tipo de preguntas den respuestas muy limitadas o que no tienen que ver con el contenido matemático. No se preocupe, se espera que poco a poco los alumnos puedan hacer análisis más profundos y que incluyan argumentos matemáticos en sus respuestas.

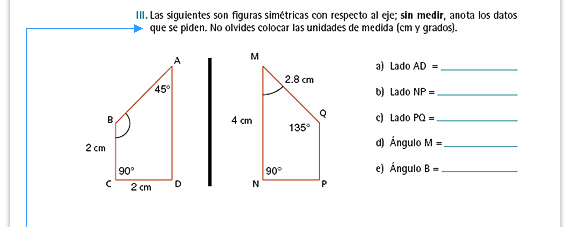
Respuestas. La medida de cada segmento debe ser igual a la medida de su simétrico; de la misma manera, la medida de cada ángulo debe ser igual a la medida del ángulo que le corresponde en la figura simétrica. Sugerencia didáctica. Si durante la confrontación del problema inicial no se propuso la medición de ángulos y de lados para verificar las respuestas, esta es una buena oportunidad para que usted lo sugiera al grupo.

Un aspecto relevante de la enseñanza de las matemáticas es que los alumnos se hagan competentes en la comunicación e interpretación de ideas, lo que implica que gradualmente se familiaricen con el lenguaje matemático; para ello será necesario que conozcan y utilicen simbología específica que les permita comunicar e interpretar ciertas ideas matemáticas. En esta parte de la sesión, además de hacer notar que la simetría con respecto a un eje conserva el paralelismo y la perpendicularidad, se introduce la notación para estos dos conceptos.

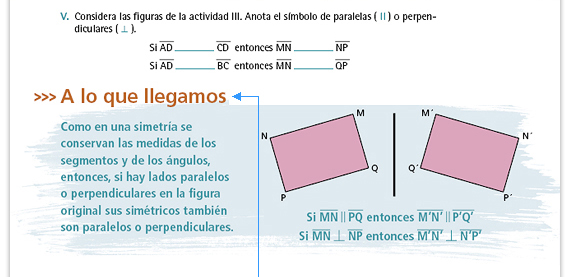
Sugerencia didáctica. Al comentar esta información haga énfasis en que la conservación de paralelas y perpendiculares es consecuencia de que la simetría conserva medidas de ángulos y de longitudes.

Propósito del video. Conocer la manera de trazar una figura simétrica con respecto a otra e identificar las propiedades que se conservan con la simetría axial.