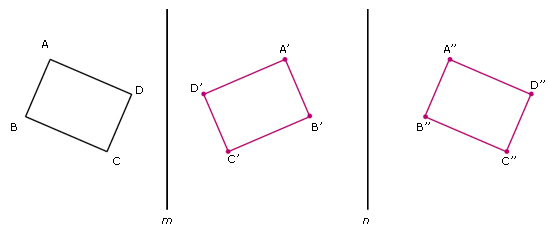
Propósito de la sesión. Practicar los conocimientos adquiridos al resolver diversos ejercicios. Organización del grupo. Es conveniente que los alumnos resuelvan estos ejercicios de manera individual; no obstante, procure que en algún momento (en la misma clase o en la clase siguiente) se abra un espacio para comparar procedimientos y resultados.

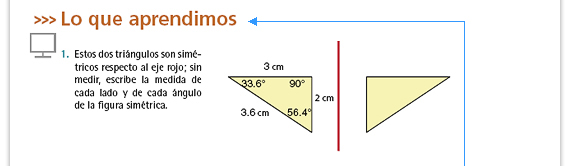
Integrar al portafolios. Con este ejercicio podrá obtener información respecto al conocimiento de los alumnos sobre el concepto de simetría, particularmente de la propiedad de preservación de las magnitudes. Los alumnos deben concluir que las medidas en el triángulo simétrico se corresponden uno a uno con las del triángulo original. Si nota alguna dificultad lean nuevamente la conclusión del recuadro A lo que llegamos de la sesión 3 y realice con ellos más ejercicios como los que se proponen en las actividades II y III del Manos a la obra de esa misma sesión. Respuestas. La medida de cada segmento debe ser igual a la medida de su simétrico; de la misma manera, la medida de cada ángulo debe ser igual a la medida del ángulo que le corresponde en la figura simétrica.

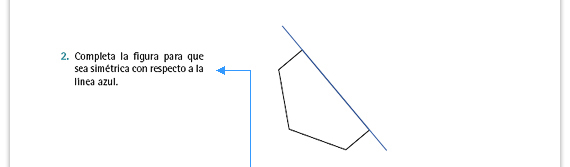
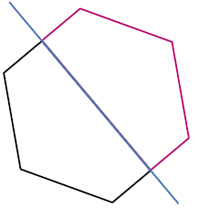
Integrar al portafolios. Observe si los alumnos logran identificar puntos y segmentos simétricos. Recuerde que en figuras poligonales es suficiente con localizar los puntos simétricos de los vértices y después unirlos mediante los segmentos adecuados. Si los alumnos muestran dificultades para resolver el ejercicio, realice con ellos más ejercicios como los que se trabajan en Manos a la obra de la sesión 2.

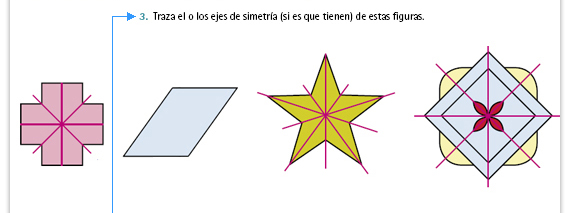
Sugerencia didáctica. El romboide es la única figura que no tiene eje de simetría, sin embargo, es posible que algunos alumnos consideren las diagonales como ejes. Si sucede eso, invítelos a verificar si se cumplen las propiedades que han estudiado.

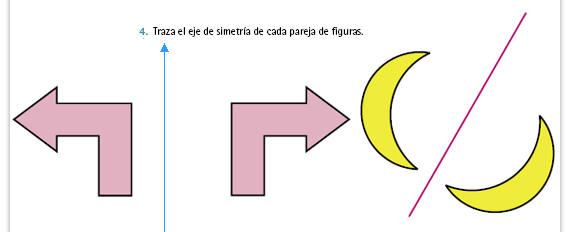
Propósito del ejercicio. Se espera que los alumnos apliquen las propiedades estudiadas en la primera sesión de la secuencia y que usen implícitamente la idea de que el eje de simetría es mediatriz de los segmentos que unen puntos simétricos (la mediatriz de un segmento es la recta perpendicular al segmento que pasa por su punto medio); aunque el tema de mediatriz corresponde al bloque 2, los alumnos pueden resolver el ejercicio con lo que han aprendido en estas lecciones.

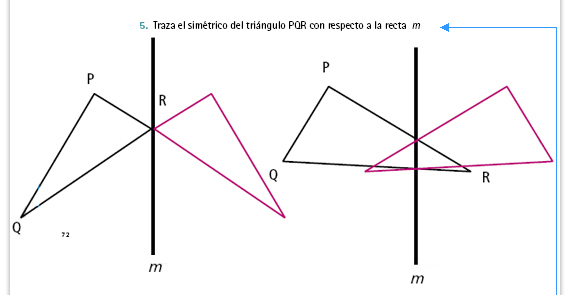
Posibles dificultades. En el segundo caso el eje de simetría cruza a la figura, por lo que es probable que sea difícil para los alumnos resolverlo; si nota que hay muchas dificultades, puede sugerirles que consideren primero la parte de la figura que está a la izquierda del eje y luego la que está a la derecha.

Propósito del ejercicio. Preparar a los alumnos para un tema que estudiarán más adelante: la composición de dos simetrías con respecto a dos ejes paralelos. Se espera que los alumnos noten que el resultado es una figura idéntica a la primera, pero que no es su simétrica.