Propósito de la sesión. Caracterizar las situaciones en las que hay cantidades directamente proporcionales, resolver algunas de esas situaciones mediante el uso de tablas y utilizar la suma y la multiplicación de cantidades directamente proporcionales como estrategias de resolución. Organización del grupo. Se sugiere trabajar toda la sesión en parejas y organizar intercambios grupales para comparar resultados y procedimientos.

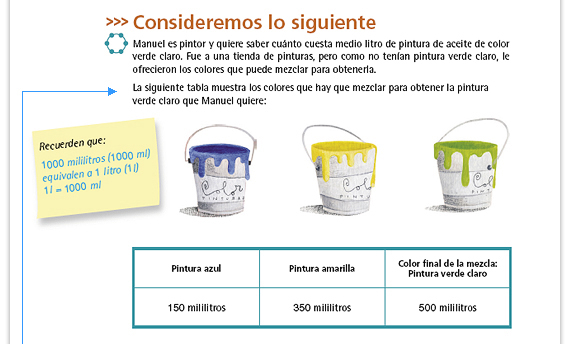
Sugerencia didáctica. Antes de que los alumnos comiencen a resolver la primera actividad, dedique unos minutos para que en parejas la lean. Posteriormente puede preguntar al grupo:"¿De qué se trata el problema?" para ver si los alumnos lo han comprendido. Procure no adelantar resultados o estrategias de solución. Posibles dificultades. El problema tiene cierta complejidad, por lo que es posible que no todos los alumnos respondan correctamente. Un posible error al tratar de obtener el costo de 500 ml de pintura verde claro es el de sumar el costo de 1 litro de pintura azul con el costo de 1 litro de pintura amarilla, sin considerar las cantidades que se indican para obtener la mezcla. Este error podrá ser corregido en la sección Manos a la obra.

Eje

Manejo de la información.

Tema

Análisis de la información.

Antecedentes

En la escuela primaria los alumnos aprendieron a distinguir situaciones de proporcionalidad directa de las que no lo son y resolvieron problemas de variación proporcional mediante distintos procedimientos. Ahora analizarán esos recursos con mayor profundidad destacando las propiedades que caracterizan a las situaciones de proporcionalidad directa.

Propósitos de la secuencia Identificar y resolver situaciones de proporcionalidad directa del tipo "valor faltante" en diferentes contextos, utilizando de manera flexible diversos procedimientos.
Sesión	Título y propósitos de la sesión	Recursos	Vínculos
1	Las cantidades directamente proporcionales Caracterizar las situaciones en las que hay cantidades directamente proporcionales, resolver algunas de esas situaciones mediante el uso de tablas y utilizar la suma y la multiplicación de cantidades directamente proporcionales como estrategias de resolución.
2	Valor unitario Utilizar el valor unitario en problemas de escalas y emplear fracciones unitarias para determinar valores faltantes en situaciones directamente proporcionales.	Video "Escalas y maquetas en arquitectura"	Geografía Secuencia 2
3	Proporcionalidad en otros contextos Aplicar el valor unitario en la solución de problemas que impliquen cantidades directamente proporcionales.	Interactivo	Ciencias Secuencia 9

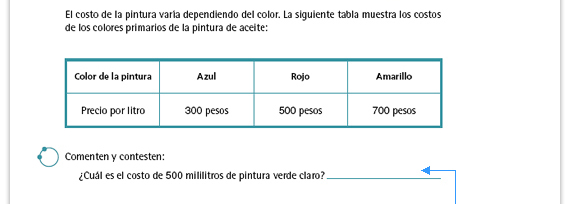
Respuestas. Una forma de resolver el problema es calculando el costo de la cantidad de pintura que se requiere de cada color. 1 litro de pintura azul cuesta $300; 100 ml cuestan $30; 50 ml cuestan $15. Entonces 150 ml de pintura azul cuestan $45. 1 litro de pintura amarilla cuesta $700; 100 ml cuestan $70; 50 ml cuestan $35. Entonces 350 ml de pintura amarilla cuestan $245. En total, 500 ml de pintura verde cuestan $290.

Sugerencia didáctica. Puede registrar en el pizarrón las respuestas de cada una de las parejas y pedirles a aquellas que hayan obtenido resultados distintos (correctos o incorrectos) que expliquen cómo resolvieron el problema.

Sugerencia didáctica. Permita que los alumnos se tomen el tiempo suficiente para comentar este procedimiento.

Propósito de la pregunta. La intención es que los alumnos se percaten de que el procedimiento seguido en la otra telesecundaria es erróneo (porque para hacer 2 litros de pintura verde claro se utilizarían 600 mililitros de pintura azul y 1 400 mililitros de pintura amarilla) y que corrijan su respuesta en caso de haber tenido el mismo error.

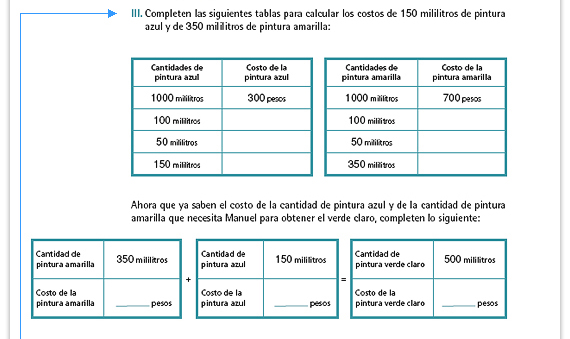
Propósito de la actividad. Al completar estas tablas se pretende que los alumnos identifiquen que en las cantidades directamente proporcionales, el aumento o La disminución de una cantidad produce un aumento o disminución proporcional en la otra. Recuerde que. Una situación de proporcionalidad directa cumple con todas las siguientes propiedades: Cuando crece una de las magnitudes, crece la otra de manera proporcional. Al aumentar la cantidad de pintura aumenta el costo de manera proporcional. Por ejemplo, si 1 000 ml de pintura azul cuestan 300 pesos, entonces 2 000 ml (que son el doble de 1 000 ml) deben costar 600 pesos (el doble de 300 pesos). A la suma de valores de una magnitud le corresponde la suma de valores de la otra magnitud. Para la pintura azul 100 ml + 50 ml = 150 ml; la suma de los costos correspondientes es igual al costo de 150 ml: $30 + $15 = $45 A diferencias iguales en una magnitud, corresponden diferencias iguales en la otra magnitud. 150 ml – 100 ml = 50 ml; la diferencia entre los costos correspondientes, es igual al costo de 50 ml: $45 - $30 = $15 El cociente entre las cantidades de un mismo renglón es siempre el mismo. 300 ÷ 1 000 = 0.3; 45 ÷ 150 = 0.3; 15 ÷ 50 = 0.3

Posibles procedimientos. Los alumnos podrían hacer una tabla como la siguiente: Otra forma de resolver es: Como 500 ml cuestan $290, 1 litro cuesta lo doble: $580; entonces 100 ml cuestan $58 ($580 ÷ 100). Se multiplica 58 × 8 para obtener el precio de 800 ml. El precio de 800 ml es $464. 120 ml de verde claro cuestan $69.60, porque como 100 ml cuestan $58 y 10 ml cuestan $5.80 pesos, entonces 20 ml cuestan $11.60. Se suma $58 + $11.60 = $69.60

Cantidad de pintura verde claro	Costo
500 ml	$290
800 ml	$464
120 ml	$69.60
100 ml	$58
1000 ml	$580

Sugerencia didáctica. Pida a los alumnos que lean esta información y que después contesten en sus cuadernos: ¿Cuándo dos cantidades son directamente proporcionales?

Sugerencia didáctica. Esta actividad puede quedar como un ejercicio para que los alumnos resuelvan en casa. En su oportunidad, cuando se revisen sus respuestas, usted puede proponer una tabla en el pizarrón para que ahí se concentren los resultados:

Cantidad de pintura verde oscuro:	Costo
500 ml	$230
800 ml	$368
120 ml	$55.20