
|

|

|
 |
 |

| Propósito de la sesión. Aplicar
el valor unitario en la solución de
problemas que impliquen cantidades
directamente proporcionales.
Organización del grupo. A lo largo de la sesión los alumnos trabajan individualmente, en parejas y en equipos de tres. |

| Respuestas. Pagó $7 porque cada caramelo cuesta $0.50 El costo de un caramelo es el valor unitario. | Propósito del interactivo. Resolver problemas que involucran cantidades directamente proporcionales utilizando la estrategia de valor unitario. |

Sugerencia didáctica. En este caso,
los alumnos no requieren obtener el
valor unitario (ese dato ya se les da
en la tabla), pero si podrían tener
dificultades al trabajar con fracciones
y con números decimales.
Puede sugerirles que escriban el 4.2
como fraccion (4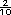 o 4 o 4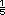 ) para que
todos sean fraccionarios. Entonces
tendrian que multiplicar cada fraccion
por 120 ) para que
todos sean fraccionarios. Entonces
tendrian que multiplicar cada fraccion
por 120 |

| Propósito de la actividad.
Se pretende que los alumnos
reconozcan una situación de variación
proporcional directa (automóvil 1)
comparándola con otra en la que
la variación no es proporcional
(automóvil 2). Estas actividades son
importantes y puede ser de utilidad
que ponga otros ejemplos.
Integrar al portafolios. Pida a los alumnos que resuelvan y copien en una hoja aparte esta actividad. Utilícela para ver qué estrategia de resolución emplean y si logran determinar la respuesta correcta. Si tienen dificultades ponga más ejercicios como el de los caramelos que aparece en esta sesión. |
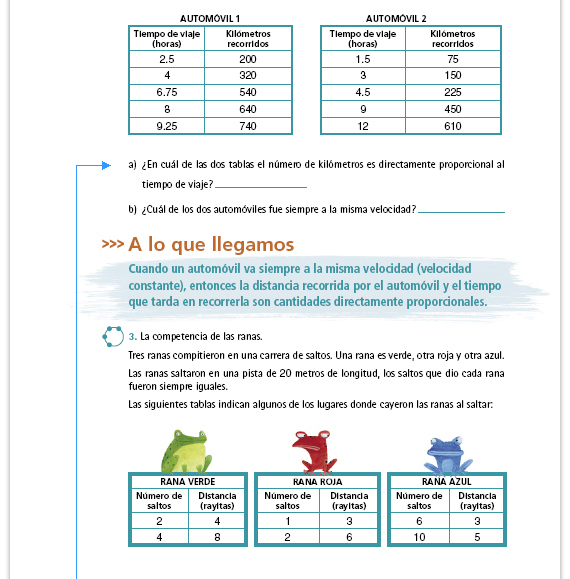
| Respuestas. El automóvil 1, por
cada hora de viaje recorre 80 km
(valor unitario) y se verifica en todos
los datos de la tabla, es decir, fue
siempre a la misma velocidad.
El automóvil 2, por cada hora de viaje recorre 50 km (valor unitario), pero en el último renglón las cantidades ya no son proporcionales, porque 12 × 50 = 600 |

Respuestas.
|
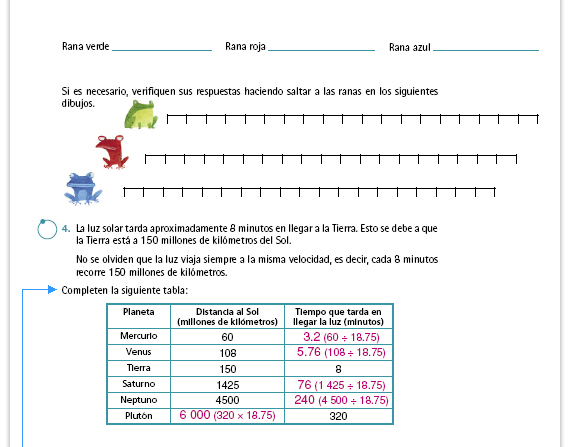
| Sugerencia didáctica. Lo más
importante en estas actividades es que
los alumnos trabajen con situaciones
de proporcionalidad directa. Puede
decirles que utilicen la calculadora
para que no se detengan mucho en
hacer las operaciones con punto
decimal.
Respuestas. Una forma económica de resolver este problema es calcular cuántos kilómetros recorre la luz del Sol en un minuto, es decir, el valor unitario. En un minuto la luz recorre 18.75 millones de kilómetros, por lo tanto, para hallar cuánto tiempo tarda en llegar la luz a Mercurio, por ejemplo, hay que encontrar un número que multiplicado por 18.75 dé 60, es decir, ____ × 18.75 = 60, que puede resolverse así: 60 ÷ 18.75 = _____ El cálculo de la distancia a la que se encuentra Plutón puede hallarse multiplicando el tiempo que la luz tarda en llegar por el valor unitario, 320 × 18.75 = ______, o bien, fijarse en los datos de la tabla. Si en 8 minutos la luz recorre 150 millones de kilómetros, en un periodo de tiempo 40 veces mayor (porque 8 × 40 = 320) recorrerá una distancia también 40 veces mayor. |

| Sugerencia didáctica. Si se dispone de aula de medios, la página referida puede ser interesante para los alumnos, ya que en ella se da información sobre el descubrimiento de un nuevo planeta llamado Zedna. |