Propósito de la sesión. Solucionar problemas sencillos de reparto proporcional mediante diversos procedimientos y utilizando tablas de cantidades directamente proporcionales. Organización del grupo. En la sesión hay trabajo individual, en parejas y momentos de intercambio grupal.

Sugerencia didáctica. El problema no es tan sencillo, es conveniente dejar que los alumnos intenten resolverlo aunque no lo consigan. Más adelante se les proporcionarán elementos para que puedan hacerlo. Respuestas. Deben tocarles, respectivamente, $150, $300 y $600

Eje

Manejo de la información.

Tema

Análisis de la información.

Antecedentes

En la secuencia anterior los alumnos identificaron y resolvieron situaciones de proporcionalidad en diversos contextos. En esta secuencia los alumnos emplearán distintos procedimientos para resolver problemas de reparto proporcional mediante ejercicios como: un grupo de personas aporta una cantidad inicial (por ejemplo, dinero que se invierte para un negocio), la ganancia obtenida habrá que repartirla proporcionalmente de acuerdo con lo que cada persona aportó.

Propósitos de la secuencia Elaborar y utilizar procedimientos para resolver problemas de reparto proporcional.
Sesión	Propósitos de la sesión	Recursos
1	La kermés Solucionar problemas sencillos de reparto proporcional mediante diversos procedimientos y utilizando tablas de cantidades directamente proporcionales.	Video "Reparto proporcional" Interactivo
2	Más sobre reparto proporcional Solucionar problemas de reparto proporcional mediante el uso del valor unitario.	Video

Sugerencia didáctica. Es interesante que los alumnos hagan comentarios sobre la situación para ir comprendiendo lo que quiere decir "hacer un reparto proporcional". Respuestas. a) Al tercer amigo no le parece bien repartirlo así porque él puso más dinero que los otros dos. b) Cuatro veces más. c) Dos veces más.

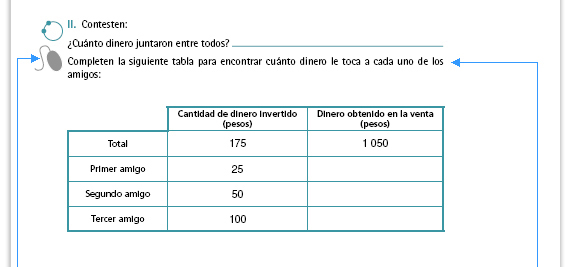
Propósito del interactivo. Resolver problemas de reparto proporcional.

Posibles procedimientos. Algunos alumnos pueden intentar completar la tabla hallando el valor unitario. Por cada peso invertido se obtuvieron 6, por lo tanto, 6 es el valor unitario. Si el primer amigo invirtió $25 su ganancia debe ser 25 × 6 Otra forma de resolverlo es fijándose en las relaciones de la tabla. Al invertir $175 se obtuvieron $1 050, y $175 entre 7 es igual a $25, por lo tanto la ganancia del primer amigo puede hallarse dividiendo 1 050 entre 7. El segundo amigo invirtió el doble que el primero, así que su ganancia deberá ser el doble.

Respuestas. El valor unitario en este caso es 120 porque cada hectárea se pagó a $120.

Sugerencia didáctica. Si ya no tiene tiempo puede dejar esta actividad como tarea y al siguiente día pedirles que en pequeños equipos comenten mediante qué procedimiento lo resolvieron y qué resultados obtuvieron. Posibles procedimientos. -Puede obtenerse el valor unitario (cada m2 se pagó a $20) y multiplicar lo que cada albañil levantó por 20. -También se pueden fijar en que el que levantó 15 m2 debe recibir la mitad del pago, el que levantó 10 m2 la tercera parte del pago y el resto es para el que levantó 5 m2. Respuestas. El que levantó 15 m2 debe recibir $300, el que levantó 10 m2 $200, y el que levantó 5 m2 $100.

Propósito del video. Determinar si un problema es o no de reparto proporcional y la parte que corresponde a cada uno de los involucrados.