
|

|

|
 |
 |

| Propósito de la sesión. Solucionar
problemas de reparto proporcional
mediante el uso del valor unitario.
Organización del grupo. Las actividades se realizan en parejas, salvo la última y cuando se sugiere comentar con los demás. |

| Sugerencia didáctica. Permita que
los alumnos utilicen el procedimiento
que prefieran y no les dé las
respuestas; si no pueden obtenerlas
aquí lo harán más adelante.
Respuestas. Juntaron $5 000 y por cada peso ganaron $20, que es el valor unitario. A Pedro le deben tocar $44 000 (2 200 × 20) y a Édgar $56 000 (2 800 × 20). |

Respuestas.
|

| Sugerencia didáctica. Solicite a los
alumnos que lean con atención el
relato o pida que uno de ellos lo lea
en voz alta.
Este problema es muy interesante, ya que aparentemente la situación que se plantea corresponde a un reparto proporcional. El reto que se presenta a los alumnos es que logren identificar y argumentar lo contrario. Sin embargo, es probable que varios alumnos concluyan que el reparto sí es proporcional. Pídales que den sus argumentos, posteriormente tendrán la oportunidad de verificar sus respuestas. |

| Propósito de la actividad. Pretende
confrontar la idea errónea de que el
reparto sí es proporcional haciendo
un análisis de la cantidad de pan que
cada viajero aportó y la cantidad que
cada uno de ellos comió.
Respuestas. En total se repartieron 8 panes entre 3 viajeros y cada viajero comió  de pan, es decir, 2 de pan, es decir, 2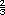 . Uno de
los viajeros aportó 3 panes, de los que
Salem se comió . Uno de
los viajeros aportó 3 panes, de los que
Salem se comió 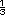 de pan; mientras
que el otro viajero aportó 5 panes, de
los que Salem se comio 2 de pan; mientras
que el otro viajero aportó 5 panes, de
los que Salem se comio 2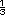 panes. Por
lo tanto, Salem debió dar 1 moneda
de oro al que aportó 3 panes, y 7
monedas al que dio 5 panes; es decir,
una moneda de oro por cada tercio de
pan que se comió. panes. Por
lo tanto, Salem debió dar 1 moneda
de oro al que aportó 3 panes, y 7
monedas al que dio 5 panes; es decir,
una moneda de oro por cada tercio de
pan que se comió.
Integrar al portafolios. Las respuestas que den los alumnos a este problema podrán darle información acerca de lo que saben sobre el reparto proporcional. Es importante considerar que en este problema hay dos elementos presentes: el manejo de fracciones y la proporcionalidad, y es posible que los alumnos tengan dificultades con uno de los dos aspectos o con ambos. Podría serles de ayuda hacer los repartos mediante representaciones de los panes con plastilina o papel. |


| Respuestas. Hay que encontrar
el valor unitario, es decir, cuántos
habitantes habría en 1 kilómetro
cuadrado. Se obtiene dividiendo
14 860 000 (el total de habitantes de
los cuatro estados) entre 79 500 (el
total de kilómetros cuadrados de los
cuatro estados), y da como resultado
186.918239 habitantes por kilómetro
cuadrado. El resultado es un número
con muchas cifras decimales que
deberá redondearse o truncarse.
Para hacer el reparto proporcional se
multiplica este valor unitario por la
extensión de cada estado.
Sugerencia didáctica. Las respuestas obtenidas son números con punto decimal porque el valor unitario no es un número entero, sin embargo, para algunos alumnos puede ser confuso el resultado. Conviene comentar qué significa que haya 373 836.478 personas por kilómetro cuadrado en Tlaxcala, y por la dificultad del cálculo se sugiere que utilicen calculadora. Otra opción es redondear el valor unitario a 187 habitantes por kilómetros cuadrados. |

| Sugerencia didáctica. Si cuentan con Internet pida a los alumnos que busquen información sobre su estado y la comparen con la de otros estados. |