Propósito de la sesión. Identificar situaciones que se resuelven mediante procedimientos de recuento o enumeración, y utilizar estrategias personales para resolverlas. Materiales. Lápices de colores. Organización del grupo. Se propone que los alumnos trabajen en parejas y que el apartado Lo que aprendimos se resuelva de manera individual.

Eje

Manejo de la información.

Tema

Representación de la información.

Antecedentes

En la escuela primaria los alumnos resolvieron problemas en los que fue necesario interpretar y organizar información presentada a través de tablas, gráficas y diagramas de árbol. En este mismo sentido, se espera que los alumnos desarrollen conocimientos y habilidades que les permitan deducir e interpretar información a partir de la que se muestra en este tipo de representaciones.

Propósitos de la secuencia Resolver problemas de conteo utilizando diversos recursos y estrategias como tablas, diagramas de árbol y otros procedimientos de enumeración.
Sesión	Propósitos de la sesión	Recursos	Vínculos
1	¿Cuántos caminos hay? Identificar situaciones que se resuelven mediante procedimientos de recuento o enumeración y utilizar estrategias personales para resolverlas.	Video "¿Saben cuántos caminos hay?" Interactivo
2	¿De cuántas formas? Explorar formas de realizar un conteo mediante tablas o diagramas de árbol.	Interactivo	Ciencias secuencia 31 ¿Cómo se heredan las características de un organismo?
3	¿Cuántos viajes hay...? Encontrar procedimientos sistemáticos de conteo en situaciones diversas; particularmente utilizar la regla del producto.	Interactivo
4	Otros contextos Interpretar procedimientos sistemáticos de conteo.	Interactivo

Propósito de las actividades. Por una parte, se pretende que los alumnos se familiaricen con el mapa, y por la otra, que exploren de manera intuitiva los posibles recorridos que podría efectuar Ana. Hay distintas respuestas, algunos recorridos pueden ser más largos o más cortos (por ejemplo, 6 Oriente y 4 Norte).

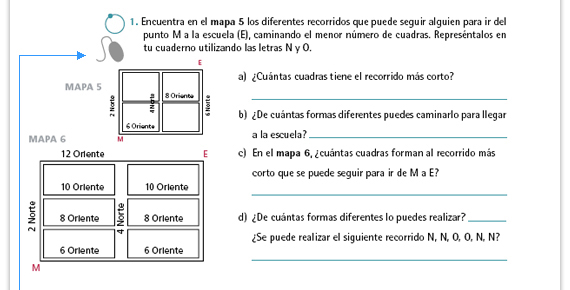
Propósito de la actividad. En esta actividad se les propone a los alumnos una representación que abstrae del mapa de la ciudad de Puebla la información necesaria y suficiente para poder encontrar los diferentes recorridos que puede seguir Ana. Se espera que los alumnos logren detectar algunas ventajas que se buscan al realizar un recorrido, como caminar el menor número de calles, lo que implica realizar el recorrido en un tiempo menor.

Respuestas. El recorrido menor es de 4 cuadras, y hay cuatro formas distintas de caminar ese recorrido.

Propósito del interactivo. Resolver problemas de conteo ocupando el procedimiento de enumeración mediante la visualización de recorridos más cortos.

Respuestas. Cada recorrido correcto tiene 3 calles hacia arriba (Norte) y una calle hacia la derecha (Oriente).

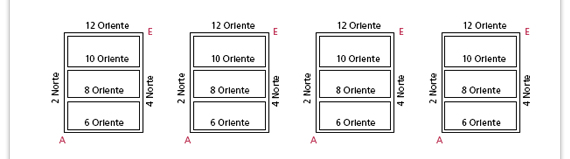
Propósito de la actividad. Se espera que los alumnos se familiaricen con dos formas de representar los recorridos, una utiliza flechas y la otra letras. De estas dos representaciones se enfatizará en las letras, pues tiene la ventaja de que al representar los recorridos se obtiene una lista en la que es muy claro reconocer aquellos que efectivamente son cortos, así como garantizar que se han obtenido todas las posibilidades. Respuestas. a) No es posible, porque un recorrido correcto sólo tiene una calle hacia el Oriente, y éste tiene dos. b) No es posible, porque un recorrido correcto tiene tres calles hacia el Norte, y éste sólo tiene dos.

Respuestas. NNNO NNON NONN ONNN

Sugerencia didáctica. Pida a los alumnos que revisen nuevamente la lista de recorridos que obtuvieron, para verificar si efectivamente en ninguno de ellos hay "regresos".

Propósito de la actividad. Se espera que los alumnos pongan en práctica los procedimientos de enumeración propuestos, y que identifiquen algunas regularidades. Respuestas. a) Por ejemplo, María está una calle más lejos que Ana y el menor número de cuadras que camina es cinco: cuatro cuadras de las calles Norte y una cuadra de las calles Oriente. b) Hay cinco formas diferentes de realizar ese recorrido: ONNNN; NONNN; NNONN; NNNON; NNNNO.

Respuesta. El menor número de cuadras que se caminan es seis: cinco cuadras de las calles Norte y una de las calles Oriente. Esta regularidad se debe a la manera en que están alineadas las calles. Hay seis maneras diferentes de hacer estos recorridos: ONNNNN; NONNNN; NNONNN; NNNONN; NNNNON; NNNNNO.

Respuestas. a) El menor número de cuadras que se caminan es cuatro, debido a la forma en que están distribuidas las calles. b) Hay seis recorridos diferentes: NNOO; NONO; NOON; ONNO; ONON; OONN. c El menor número de cuadras que se deben caminar son cinco. d) Hay diez recorridos diferentes. No se puede realizar el recorrido N,N,O,O,N,N, porque en cualquier recorrido corto sólo se caminan tres cuadras hacia el Norte y dos hacia el Oriente.

Propósitos interactivo. Resolver problemas de conteo ocupando el procedimiento de enumeración mediante la visualización de recorridos más cortos.

Sugerencia didáctica. Después de leer y comentar la información puede solicitar a los alumnos que redacten en sus cuadernos otras situaciones (una o dos) en las sea necesario llevar a cabo procesos de conteo. Invítelos a sugerir algunas formas de enumerar. Recuerde que. Los problemas de conteo se presentan en situaciones en las que debemos responder a la pregunta: ¿de cuántas maneras se puede resolver? En esta secuencia se trabaja con tres formas de resolver los problemas de conteo: enumeración, tablas y diagramas de árbol. La enumeración consiste en hacer una lista ordenada de todas las formas en las que podemos resolver el problema. Es importante encontrar una manera sistemática que nos permita hacer la lista y con la que podamos distinguir un resultado de otro, así como garantizar que hemos obtenido todos los resultados posibles.