
|

|

|
 |
 |

| Propósito de la sesión. Resolver
problemas que implican a la fracción
como operador multiplicativo.
Organización del grupo. Se recomienda trabajar en parejas durante toda la sesión, y de manera individual el apartado Lo que aprendimos. |

Propósito de la actividad. Que
los alumnos resuelvan un problema
que implica la multiplicación por
una fracción, recurriendo a un
procedimiento que puede resultarles
familiar: por ejemplo, 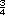 de 24 puede
resolverse dividiendo 24 entre 4 y
multiplicando por 3. Se espera que
los alumnos generen diferentes
procedimiento de resolucion que les
permitan identificar que sucede con la
multiplicacion de una fraccion por un
entero. de 24 puede
resolverse dividiendo 24 entre 4 y
multiplicando por 3. Se espera que
los alumnos generen diferentes
procedimiento de resolucion que les
permitan identificar que sucede con la
multiplicacion de una fraccion por un
entero. |

| Posibles procedimientos. Los alumnos pueden usar varias formas para calcular la cantidad que se debe pagar para cada caso, incluso es posible que recurran al cálculo mental en varias de las situaciones. |
| Eje |
| Sentido numérico y pensamiento algebraico |
| Tema |
| Significado y uso de las operaciones. |
| Antecedentes |
| En la escuela primaria los alumnos no trabajaron la multiplicación y división de fracciones, por lo que éste constituye un nuevo conocimiento. El tipo de situaciones que se les plantea en esta secuencia, se ubican en el contexto de la proporcionalidad; es decir, se trata de situaciones en las que los alumnos deben establecer una relación proporcional entre dos magnitudes y decidir cuál de estos términos se va a calcular. La resolución de esas situaciones implica la multiplicación o división de fracciones. |
| Propósitos de la secuencia
Resolver problemas que impliquen la multiplicación y división con números fraccionarios en distintos contextos. |
||
| Sesión | Título y propósitos de la sesión | Recursos |
| 1 | De compras en el mercado. Resolver problemas que implican a la fracción como operador multiplicativo. | Video "¿Dónde se utilizan las fracciones?" Interactivo |
| 2 | Superficies y fracciones. Multiplicar números fraccionarios a partir del cálculo del área de rectángulos cuyos lados son medidas fraccionarias. Conocer el algoritmo de la multiplicación de fracciones. | Interactivo |
| 3 | ¿Cómo serían las marcas atléticas en el espacio? Resolver problemas que impliquen la división de fracciones. Interpretar y dar significado a dividir un entero entre una fracción, un número mixto y una fracción. Relacionar la división de fracciones con la multiplicación de un entero o fracción por el recíproco del otro factor (fracción). | Video "El sistema solar y la fuerza de gravedad" Interactivo |
| 4 | Hay tela de donde cortar. Resolver problemas que implican una división de fracciones y analizar el resultado, es decir, identificar cuándo es mayor o menor a los números que se están operando. | |

Propósito de la actividad. Los
procedimientos que se presentan
para algunas de las mercancias
(como en el caso de los jitomates),
tienen la finalidad de que los
alumnos identifiquen otra forma de
interpretar la relación entre el número
fraccionario y el número entero:
2 es igual a dos veces 9, más la
mitad de 9. Otra forma de interpretarlo
es dos veces y media el número 9. es igual a dos veces 9, más la
mitad de 9. Otra forma de interpretarlo
es dos veces y media el número 9. |

Propósito del ejercicio: Identificar
que la situacion implica calcular
"cuántas veces" incrementa una
cantidad. Asi, si 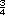 de kilo es 3 veces
también será tres veces que el que
corresponde a de kilo es 3 veces
también será tres veces que el que
corresponde a 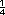 . .
Sugerencia didáctica. Otra forma de resolver es la que se muestra en el caso de las fresas. Para ese procedimiento es importante que a los alumnos les quede clara la expresión "por 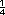 de fresas se pagan 6 pesos":
si un kilo cuesta $24, entonces un
cuarto de kilo costará la cuarta
parte de $24; esto se expresa con la
fracción de fresas se pagan 6 pesos":
si un kilo cuesta $24, entonces un
cuarto de kilo costará la cuarta
parte de $24; esto se expresa con la
fracción 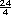 (es decir, $6). Siguiendo
este procedimiento, el costo que
corresponde a (es decir, $6). Siguiendo
este procedimiento, el costo que
corresponde a 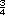 de kilo de fresa, es: de kilo de fresa, es:
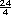 + + 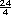 + +
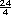 = = 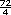 = 18,
que equivale a
6 + 6 + 6 = 18, o = 18,
que equivale a
6 + 6 + 6 = 18, o 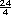 x 3, que también
puede ser 6 x 3. x 3, que también
puede ser 6 x 3. |

| Sugerencia didáctica. Pida a las parejas que comparen sus resultados con los que obtuvieron en el apartado Consideremos lo siguiente. |

| Sugerencia didáctica. Mientras los alumnos resuelven, trate de identificar los procedimientos que emplean. En el momento de la confrontación dé prioridad a aquellos procedimientos que recurren a la multiplicación de manera más clara; en caso de no presentarse ninguno, elija aquellos que permitan su generación, por ejemplo, 16 + 16 + 16 pude plantearse como 16 × 3. |
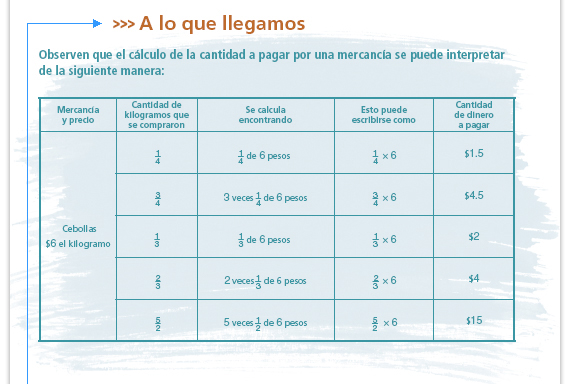
 Algo que usted puede resaltar de la
tabla, es que la expresión
Algo que usted puede resaltar de la
tabla, es que la expresión 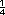 de 6,
equivale a multiplicar de 6,
equivale a multiplicar 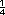 de 6, como
se expresa en la penultima columna.
Comente que hay varias formas de
resolver esa multiplicacion y que
ellos emplearon algunas al resolver el
apartado Consideremos lo siguiente. de 6, como
se expresa en la penultima columna.
Comente que hay varias formas de
resolver esa multiplicacion y que
ellos emplearon algunas al resolver el
apartado Consideremos lo siguiente.
Recuerde que. Las fracciones pueden tener distintos significados de acuerdo con las situaciones en las que se ponen en juego. En este caso, la fraccion aparece multiplicando a otro número; es un operador multiplicativo. En la escuela primaria los alumnos asociaron la multiplicacion con la obtencion de un producto que es mas grande que cualquiera de los factores. Ahora veran que cuando uno de los factores es un número fraccionario, el producto es menor, a excepcion de cuando el operador multiplicativo es una fraccion impropia (  de 6, por
ejemplo). de 6, por
ejemplo).
Sugerencia didáctica. Pregunte a los alumnos por qué sólo en el último caso de la tabla el producto es mayor que el número entero ($6). Una forma de explicarlo es la siguiente: al multiplicar una fracción propia por cualquier número, el producto es menor que ese número porque se toma sólo una parte de él; si se multiplica una fracción impropia por cualquier otro número, el producto es mayor que este número, porque se toma más de una vez. |

Posibles procedimientos.
Si no se presentara ninguno de los procedimientos anteriores, usted puede mostrarlos al grupo.
Multiplicamos 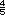 x 100 = 80. x 100 = 80.
La parte del total que esos alumnos representan se obtiene multiplicando 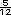 x x 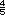 = =
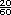 = = 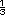
También podemos comparar 80 con 240; es la tercera parte. |

| Propósito del problema. Que los alumnos enfrenten situaciones que implican recurrir a la división como operación inversa de la multiplicación; se pretende que a partir de las estrategias que utilizaron para multiplicar una fracción por un entero, encuentren la fracción (el operador multiplicativo) que permite obtener la cantidad de dinero que se pagó. |
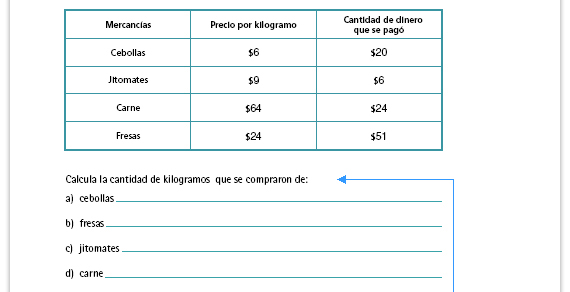
| Respuestas. En todos los casos se
divide el dinero que se pagó entre la
cantidad de kilos.
Cebollas: 3 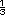 kg. kg.
Fresas: 2 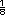 kg.
Jitomates: kg.
Jitomates: 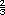 kg. kg.
Carne:  kg. kg.
Posibles procedimientos: Probablemente varios alumnos quieran resolver utilizando el algoritmo de la división con números decimales, pero les será difícil poder interpretar los resultados (algunos de los cocientes son números decimales periódicos, como 20 ÷ 6 = 3.333). Invítelos a trabajar utilizando las fracciones. Los siguientes son ejemplos de algunos procedimientos:
Entonces con $20 se compran 3 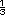 kg
de cebollas. kg
de cebollas.
Si nota que los alumnos tienen muchas dificultades para resolver, usted puede explicar y sugerir que utilicen alguno de los procedimientos anteriores. |
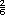 de 144
(total de aprobados)
es igual a
de 144
(total de aprobados)
es igual a 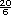 =
= 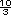 =
3
=
3