
|

|

|
 |
 |

| Propósitos de la sesión: Multiplicar
números fraccionarios a partir del
cálculo del área de rectángulos cuyas
medidas de los lados están expresadas
en fraciones.
Conocer el algoritmo de la multiplicación de fracciones. Organización del grupo. Se recomienda trabajar en parejas durante toda la sesión, intercalando con momentos de discusión grupal |
|
Propósito de la actividad. A
partir de la resolución de problemas
con los que los alumnos ya están
familiarizados (cálculo de áreas), se
espera que identifiquen el algoritmo
de la multiplicación de fracciones
utilizando distintos recursos.
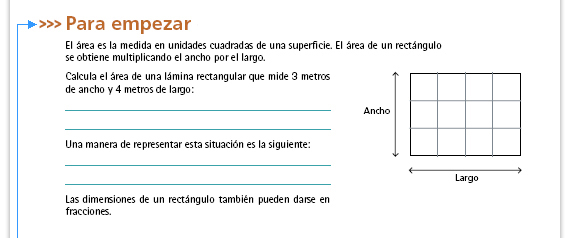
Sugerencia didáctica. Usted puede iniciar preguntando a sus alumnos cómo se calcula el área de un rectángulo; posteriormente pueden leer y comentar la información que aquí se les presenta. Particularmente es importante que cuenten y verifiquen en el dibujo el número de unidades cuadradas que conforman el área del rectángulo. |
| Posibles dificultades. Seguramente
los alumnos identificarán que el
problema se resuelve multiplicando
el largo por el ancho de cada uno
de los rectángulos, pero es muy
probable que la mayoría no sepa
cómo resolver una multiplicación
con números fraccionarios. Por ello
es necesario que los anime a buscar
una forma de calcular el área. No se
preocupe si no terminan o si lo hacen
de manera incorrecta, lo importante
en este momento es que se enfrenten
al problema de cómo resolver
una multiplicación con números
fraccionarios.
Posibles procedimientos. A partir del ejemplo anterior, tal vez algunos alumnos intenten una resolución gráfica; sin embargo, tendrían que "reconstruir" el entero (como se muestra en el apartado Manos a la obra). El algoritmo de la multiplicación de fracciones no se estudia en la escuela primaria, pero algunos alumnos podrían conocerlo o tener alguna referencia. Posibles errores.
Respuestas. Vidrio 1: 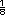 m2 m2
Vidrio 2:  m2 m2
Vidrio 3: 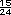 m2 o m2 o  m2 m2
|
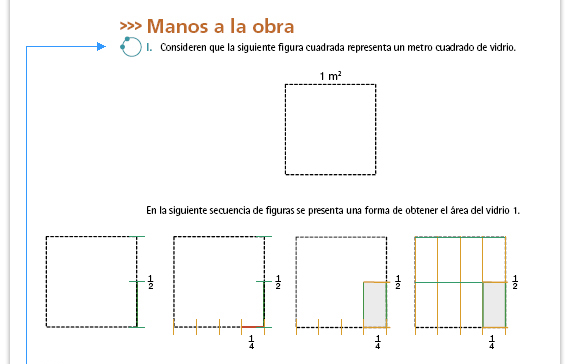
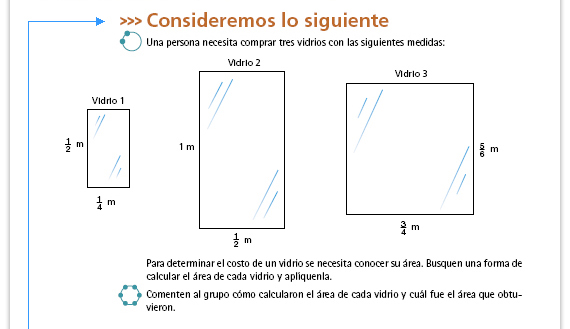
 Dé un tiempo para que las parejas
analicen la secuencia de figuras que
representa el cálculo del área del
vidrio 1 y para que respondan las
preguntas. Posteriormente invite
a una o dos parejas para que, de
manera breve, comenten al grupo
sus respuestas y cómo interpretan la
secuencia de dibujos. Posteriormete
pida a los alumnos que utilicen el
mismo recurso (el modelo de áreas)
para encontrar el área de las demás
superficies rectangulares.
Dé un tiempo para que las parejas
analicen la secuencia de figuras que
representa el cálculo del área del
vidrio 1 y para que respondan las
preguntas. Posteriormente invite
a una o dos parejas para que, de
manera breve, comenten al grupo
sus respuestas y cómo interpretan la
secuencia de dibujos. Posteriormete
pida a los alumnos que utilicen el
mismo recurso (el modelo de áreas)
para encontrar el área de las demás
superficies rectangulares. |
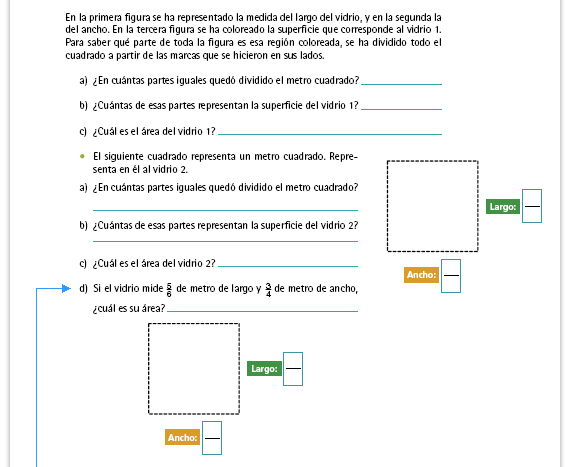
| Sugerencia didáctica: Indique a las parejas que una vez que hayan concluido, regresen al problema inicial para que revisen las respuestas que en ese momento dieron, y para que corrijan en caso de que detecten errores. |

| Propósito del interactivo. Utilizar el modelo de áreas para representar la multiplicación de fracciones. | Propósito de la actividad. En esta
situación se muestra la manera en que
se utiliza el modelo de áreas cuando se
está representando una medida mayor
a un entero.
Sugerencia didáctica. Reproduzca en el pizarrón el dibujo de los 3 metros cuadrados, pida a los alumnos que lean y comenten de qué se trata el problema. Invite a algunos alumnos a que pasen al pizarrón a calcular el área que se solicita. Una vez que todo el grupo esté de acuerdo con el resultado, pídales que resuelvan en sus cuadernos los otros dos problemas. Si el tiempo no es suficiente, puede dejarlos de tarea. Respuestas.
|

| Sugerencia didáctica. Si lo considera necesario, comente con los alumnos cómo se resuelve la multiplicación que aquí se muestra. |
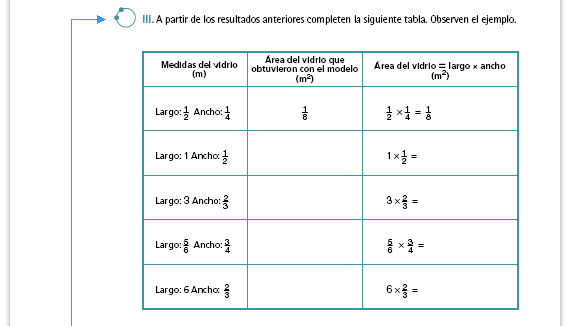
| Sugerencia didáctica. Mientras los alumnos completan la tabla, reprodúzcala en el pizarrón para que, una vez que la mayor parte de las parejas hayan terminado, pasen algunas de ellas al pizarrón a escribir y comparar sus resultados. |
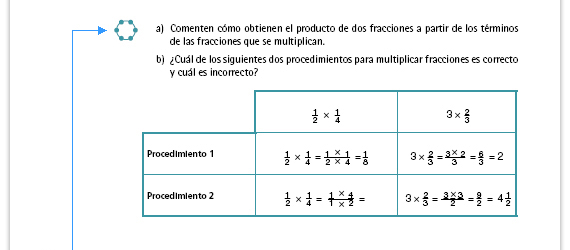
| Sugerencia didáctica. El inciso b puede ser resuelto en grupo. Es importante que los alumnos argumenten por qué consideran que uno u otro procedimiento es correcto. Para verificar sus respuestas, sugiérales que lean la información que aparece en el recuadro A lo que llegamos. |
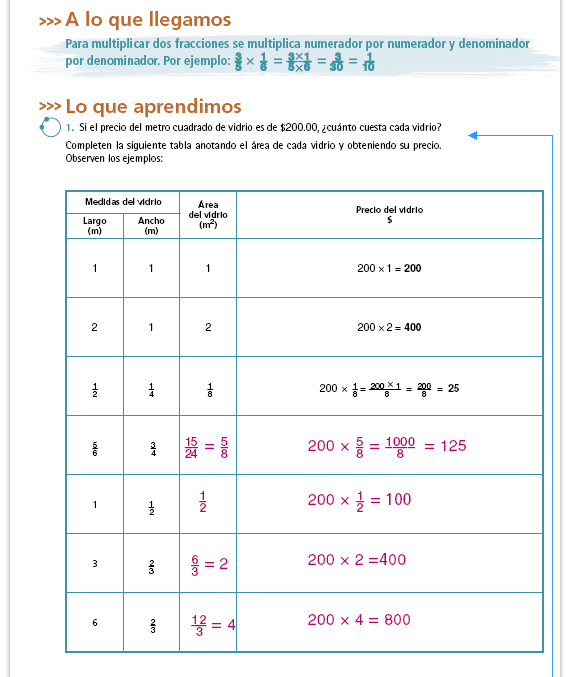
| Sugerencia didáctica: Recomiende a sus alumnos que, en lo posible, simplifiquen las fracciones para que los cálculos sean más sencillos. |
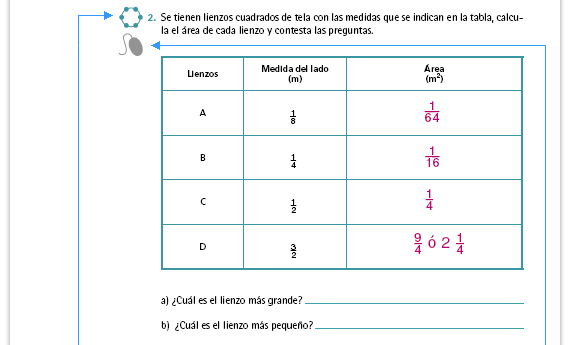
| Sugerencia didáctica: Si lo considera
necesario, recuerde a los alumnos que
el área de un cuadrado se obtiene
multiplicando lado por lado.
Respuestas. El lienzo más grande es
el D y el más pequeño es el A.
Respuestas. El lienzo más grande es el D y el más pequeño es el A. |
Propósito del interactivo: Utilizar el modelo de áreas para representar la multiplicación de fracciones. |

Respuestas.
|
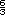 o 2 m2
o 2 m2
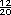 o
o

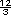 4m2
4m2 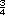 partes de la parcela. Se
multiplica
partes de la parcela. Se
multiplica 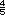 =
=
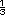 parte de la
parcela: Se araron
parte de la
parcela: Se araron 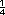 de la parcela esta
sin arar. Se multiplica
de la parcela esta
sin arar. Se multiplica 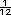
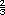 x
x 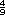 de km2
de km2