
|

|

|
 |
 |

| Propósito de la sesión. Resolver
problemas que impliquen la división de
fracciones.
Interpretar y dar significado a dividir
un entero entre una fracción, un
número mixto (fracción impropia)
entre una fracción.
Relacionar la división de fracciones con la multiplicación de un entero o fracción por el recíproco del otro factor (fracción). Organización del grupo. Se sugiere trabajar en parejas durante toda la sesión. |
Posibles procedimientos. Los
problemas que aqui se presentan
implican responder a las preguntas:
"Cuantas veces cabe 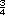 en 1m?" y
¿Cuantas veces cabe en 1m?" y
¿Cuantas veces cabe 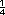 en 3 en 3 ?"
Ambas preguntas se resuelven
mediante una division de fracciones,
pero es poco probable que los alumnos
identifiquen esa operacion en este
momento.
?"
Ambas preguntas se resuelven
mediante una division de fracciones,
pero es poco probable que los alumnos
identifiquen esa operacion en este
momento.
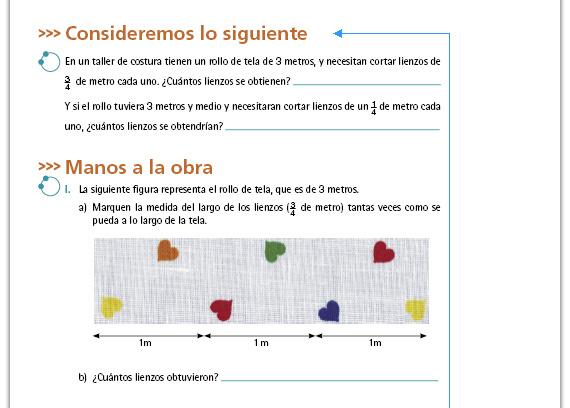
Una forma en la que pueden resolver el problema inicial es dibujar un segmento de 3 unidades, dividir cada unidad en cuartos (12 cuartos en total) y hacer marcas cada 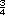 ; obteniendo 4
segmentos de esa medida. ; obteniendo 4
segmentos de esa medida.
Para el segundo problema pueden convertir 3  en cuartos, obteniendo en cuartos, obteniendo
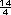 ; por lo tanto, se obtienen 14 lienzos
de ; por lo tanto, se obtienen 14 lienzos
de 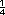 m cada uno. m cada uno.
|

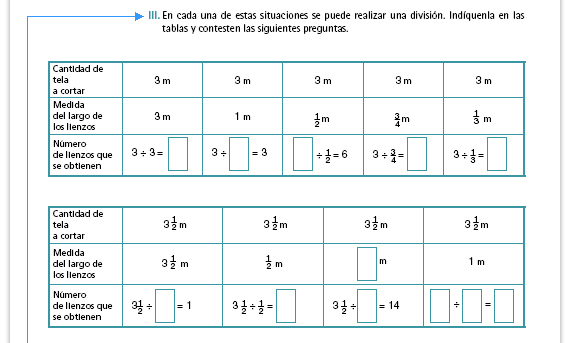
| Propósito de la actividad.
Identificarán que entre más
pequeña sea la fracción, obtendrán
un número mayor de lienzos, pero el
tamaño de ellos será menor.
Respuestas. En la mayoría de los casos la división es exacta (no hay residuo), a excepción de la segunda columna ("sobra" un metro, lo que podría desconcertar a los alumnos). Habrá que insistir en que la medida de los lienzos debe ser la indicada. |
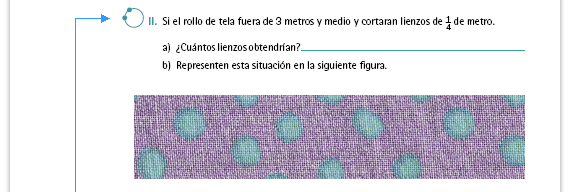
Respuesta. Puesto que la tela mide
3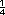 m, una forma de resolver es
convertir a fraccion impropia para
obtener m, una forma de resolver es
convertir a fraccion impropia para
obtener 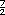 , y luego dividir la figura
en 7 , y luego dividir la figura
en 7 . Posteriormente cada medio
puede dividirse en cuartos. En total se
obtiene 14 partes de . Posteriormente cada medio
puede dividirse en cuartos. En total se
obtiene 14 partes de 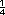 m cada una. m cada una. |
| Propósito de la actividad. Se espera que mediante el análisis de esta tabla los alumnos identifiquen que el problema que resolvieron mediante distintos recursos implica una división de fracciones. |

| Propósito de la actividad. Que le
den significado a dividir un entero
o cualquier número mixto entre una
fracción; que identifiquen qué sucede
con el resultado. La pregunta del inciso
d permite a los alumnos recordar
que dividir es la operación inversa de
multiplicar.
Respuestas.
|
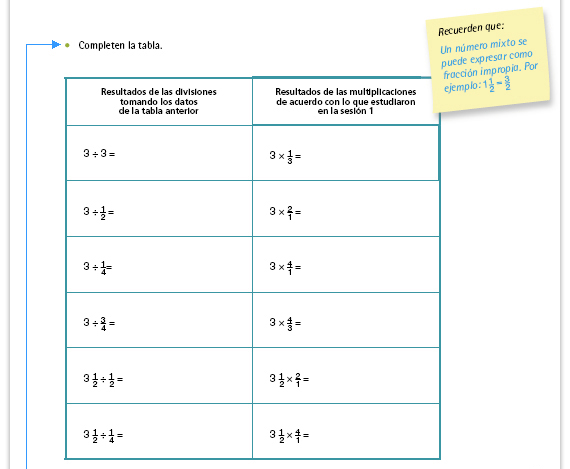
| Propósito de la actividad. Se espera que los alumnos establezcan relaciones entre la multiplicación y la división de fracciones (las cuales son operaciones inversas). Particularmente, deben identificar que al dividir un número (dividendo) entre una fracción (divisor), el resultado (cociente) es igual al que se obtiene al multiplicar el número (dividendo) por el recíproco de la fracción (divisor). |

| Propósito de la actividad. Identificarán que entre más prqueña sea la fracción, obtendrán un número mayor de lienzos, pero el tamaño de ellos será menor. |

Respuesta. El resultado es 1.
Se obtiene 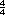 = 1. = 1. |

 Como una forma de reflexionar sobre
la información que se presenta en
el recuadro, retome alguno de los
problemas que resolvieron al inicio
con otros procedimientos, y pídales
que apliquen el algoritmo, para
verificar si obtienen el mismo
resultado.
Como una forma de reflexionar sobre
la información que se presenta en
el recuadro, retome alguno de los
problemas que resolvieron al inicio
con otros procedimientos, y pídales
que apliquen el algoritmo, para
verificar si obtienen el mismo
resultado. |
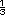 m de
largo. La division es 3 entre
m de
largo. La division es 3 entre 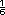 m de
largo cada uno. Por lo que en
3 m se obtienen 18 lienzos de
m de
largo cada uno. Por lo que en
3 m se obtienen 18 lienzos de