
|

|

|
 |
 |

| Propósito de la sesión. Resolver
problemas que implican una división
de fracciones y analizar el resultado,
es decir, identificar cuándo es mayor
o menor a los números que se están
operando.
Organización del grupo. Se sugiere que la sesión se trabaje en parejas y que el apartado Lo que hemos aprendido sea resuelto de manera individual. |

Posibles procedimientos. El
problema inicial se resuelve mediante
la division 5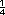 ÷ 14, y los alumnos
pueden resolver esa division de
distintas formas (una de ellas es el
algoritmo que consiste en multiplicar a
la fracción por su recíproco). ÷ 14, y los alumnos
pueden resolver esa division de
distintas formas (una de ellas es el
algoritmo que consiste en multiplicar a
la fracción por su recíproco).
Una forma de resolverlo es la siguiente: 5 litros y un cuarto de jugo son 21 cuartos de litro, pero al repartir en 14 botellas no todas tendrían la misma cantidad de jugo. Si los cuartos se transforman en octavos, serían 42 octavos de litro, que al repartirse entre 14 botellas, cada botella tendría  de
litro. de
litro.
Otra forma es aplicando el algoritmo: 5 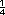 ÷ 14 = ÷ 14 =
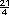 ÷ ÷ 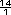 = = 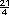 x
x 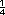 = = 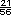 = =

|
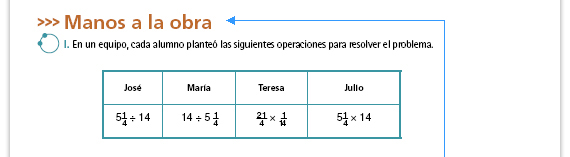
| Propósito de la actividad. Al
finalizar esta actividad, y como
consecuencia de lo que estudiaron en
la sesión anterior, se espera que los
alumnos no tengan dificultades para
reconocer qué operación efectuar o
cuáles son operaciones equivalentes
(la de "José" y la de "Teresa").
Sugerencia didáctica. Al analizar las distintas formas de plantear la división se pretende que los alumnos identifiquen errores que posiblemente ellos mismos han cometido, por lo que es importante que usted organice un intercambio grupal de respuestas y comentarios al término de esta actividad. |

| Sugerencia didáctica. Esta actividad permite que los alumnos analicen y establezcan relaciones entre los datos del problema. Usted puede recuperar algunos de los problemas que anteriormente resolvieron los alumnos y solicitarles que hagan el mismo análisis. |

| Sugerencia didáctica. Recomiende a sus alumnos que primero conviertan los números mixtos a fracciones impropias, y que en lo posible simplifiquen fracciones para que los cálculos sean más sencillos. |

| Incorporar al portafolios. Elija
algunos de estos problemas (pueden
ser los tres primeros, por ejemplo)
para que los alumnos los resuelvan
en una hoja que puedan entregarle.
Pídales que no borren las operaciones
o los dibujos que hagan, pues eso
le servirá a usted para identificar
sus procedimientos y sus posibles
errores. Si identifica que aún tienen
dificultades, repase junto con ellos
el apartado A lo que llegamos de la
sesión 4 y pida a algunos alumnos
(o hágalo usted) que muestren
en el pizarrón cómo se resuelven
correctamente esos problemas.
Respuestas.
|

| Respuestas. Se dividen los metros entre la cantidad de listón para hacer un moño. |
 litros entre 4 personas =
litros entre 4 personas =  de
litro. Esto es 2
de
litro. Esto es 2 ÷ 4,
÷ 4,
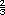 veces las calorías que
contiene un jugo de manzana. Es
decir, si se conocen las calorías del
jugo de manzana, se multiplican
por 1
veces las calorías que
contiene un jugo de manzana. Es
decir, si se conocen las calorías del
jugo de manzana, se multiplican
por 1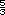 equivale a
40 x
equivale a
40 x  =
= 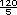 = 24. Esto significa
que un jugo de manzana tiene 24
calorías.
= 24. Esto significa
que un jugo de manzana tiene 24
calorías.
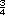 km
por hora.
km
por hora. minutos.
Si da 3
minutos.
Si da 3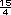 = 32 x
= 32 x 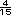 =
=
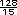 = 8
= 8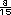
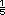 son 48
estudiantes. En total son 240
estudiantes. También se divide 144
entre
son 48
estudiantes. En total son 240
estudiantes. También se divide 144
entre