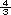|

|

|
 |
 |

| Propósito de la sesión. Dar sentido al
significado de multiplicar por un número con
punto decimal; en particular, reconocer que
al multiplicar por un número menor que la
unidad el producto es menor que los factores.
Conocer distintas formas de resolver
multiplicaciones de números decimales.
Organización del grupo. El trabajo es en parejas, salvo en la última actividad y en los intercambios grupales |
| Sugerencia didáctica. Recuerde junto con los alumnos la noción de escala, la manera en que se interpreta y cómo se encuentran las medidas reales. |

| Propósito de la actividad. Se espera que gradualmente los alumnos establezcan que aumentar una medida "tres veces y media" implica multiplicar esa medida por 3.5. Por eso, en este momento NO debe permitir que usen calculadora, pues difícilmente se percatarían de ello. Si lo considera necesario, auxílielos en la realización de los trazos, ya que por el momento éstos no son el objeto de estudio. |
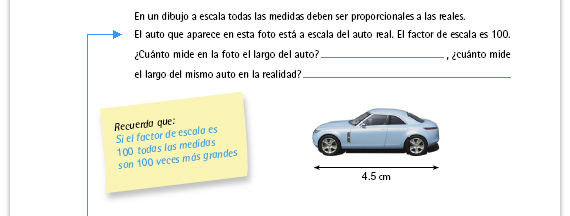
| Posibles procedimientos. Entre los diversos
procedimientos que se espera utilicen los
alumnos está la suma, ya sea mentalmente o
por escrito; por ejemplo, tres veces y media
el 6.
6 + 6 + 6 + 3 = 21 También es probable que quienes ya saben que 3.5 × 6 es lo mismo que 6 × 3.5, decidan sumar 6 veces el 3.5 3.5 + 3.5 + 3.5 + 3.5 + 3.5 + 3.5 = 21 Dado que en la primaria los alumnos aprendieron a multiplicar decimales, habrá quienes hagan uso del algoritmo convencional. 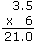
Se espera que, conforme vayan resolviendo las actividades, los alumnos noten que la multiplicación es la más eficaz. |
| Eje |
| Sentido numérico y pensamiento algebraico. |
| Tema |
| Significado y uso de las operaciones. |
| Antecedentes |
| En la escuela primaria los alumnos utilizaron la multiplicación de números decimales al resolver problemas de proporcionalidad directa, particularmente al utilizar el valor unitario y al calcular áreas de rectángulos. En ese contexto reflexionaron sobre el significado de esa operación y de su resultado. En el primer grado de la escuela secundaria los alumnos fortalecerán esos significados y los aplicarán a otros contextos. |
| Propósitos de la secuencia
Resolver problemas que impliquen la multiplicación de números decimales en distintos contextos. |
||
| Sesión | Título y propósitos de la sesión | Recursos |
| 1 | Tres veces y media Dar sentido al significado de multiplicar por un número con punto decimal; en particular, reconocer que al multiplicar por un número menor que la unidad el producto es menor que los factores. Conocer distintas formas de resolver multiplicaciones de números decimales. | Video"Más de tres, pero menos de cuatro" Interactivo |
| 2 | El punto es el asunto Conocer y practicar la técnica para multiplicar números decimales. | Interactivo |
| 3 | ¿En dónde se usa la multiplicación de decimales? Resolver problemas diversos que implican multiplicar números decimales. | |

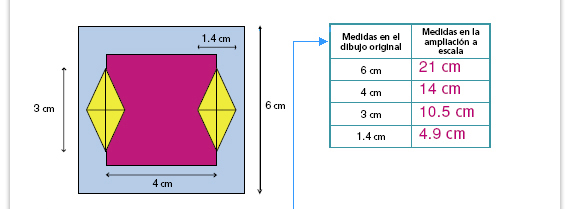
 Sugerencia didáctica. En la
confrontación NO es importante
que digan cómo trazaron la figura,
sino cómo hicieron los cálculos para
obtener las medidas de la copia a
escala.
Sugerencia didáctica. En la
confrontación NO es importante
que digan cómo trazaron la figura,
sino cómo hicieron los cálculos para
obtener las medidas de la copia a
escala. |

| Propósito de la actividad. El propósito es afianzar la idea de que calcular tres veces y media un número es igual a multiplicarlo por 3.5. |
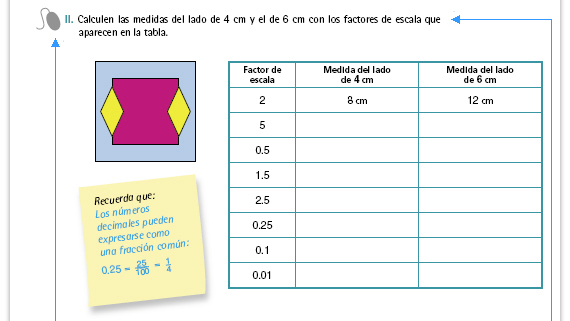
| Propósito de la actividad. Con la actividad II se pretende que los alumnos exploren y reflexionen acerca de lo que sucede cuando se multiplica por un número menor que la unidad. En el caso de los números naturales el producto siempre es mayor o igual que cualquiera de los factores (4 × 5 = 20, 22 × 1 = 22), por ello es muy común que los alumnos piensen que con los decimales pasa lo mismo. Cuando una cantidad se multiplica por un número menor que 1 el producto es menor que esa cantidad. Saber lo que sucede cuando se hacen multiplicaciones con números decimales contribuye a que los alumnos desarrollen su sentido numérico (por ejemplo, para hacer cálculos y verificar resultados). | Respuestas.
|

Respuestas.
|

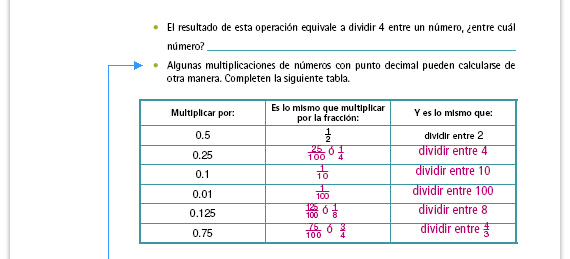
| Propósito de la actividad. Es muy importante que los alumnos aprendan a decidir cuál es la mejor manera de resolver una operación. Por ejemplo, para resolver 200 × 0.25 es más fácil sacar cuarta a 200 que hacer la multiplicación. Con esta actividad (III) se pretende que los alumnos concluyan que no siempre es necesario hacer una multiplicación para saber el resultado y que muchas veces es más rápido y sencillo resolverla de otra manera. Enfatice esta idea con los alumnos en el momento de la confrontación. |
| Integrar al portafolios. Si
tienen dificultades hagan más
multiplicaciones por números menores
que 1 y analicen los resultados.
Respuestas. El último caso (el de 0. 75) es más difícil que los anteriores porque hay varias respuestas que involucran más operaciones, no sólo dividir:
Es probable que no lleguen a ninguna, en la confrontación de resultados recuerde junto con ellos lo que estudiaron en la secuencia 10 (Multiplicación y división de fracciones). |

Posibles procedimientos. Entre las
maneras con que puede calcular 0.75
× 4 están:
Sugerencia didáctica. Los alumnos deben desarrollar su capacidad para decir cuál es la manera más conveniente de resolver una operación: utilizando el algoritmo convencional, la calculadora o el cálculo mental. Invítelos continuamente a comentar en qué situaciones elegirían una u otra forma de resolución. |

| Sugerencia didáctica. La práctica del cálculo mental debe estar presente continuamente en las clases de matemáticas, ya que permite descubrir muchas relaciones entre los números desarrollando el sentido numérico y el de las operaciones. Invite a los alumnos a que, efectivamente, resuelvan con cálculo mental estas operaciones y en el momento de la confrontación comenten los procedimientos que usaron. |

 Sugerencia didáctica. Lea y
comente junto con los alumnos esta
información, puede pedirles que lo
transcriban en su cuaderno y que
ejemplifiquen cada afirmación con
una operación distinta a la enunciada,
después pueden comentar los ejemplos
que hayan escrito para enriquecer el
apunte de todos.
Sugerencia didáctica. Lea y
comente junto con los alumnos esta
información, puede pedirles que lo
transcriban en su cuaderno y que
ejemplifiquen cada afirmación con
una operación distinta a la enunciada,
después pueden comentar los ejemplos
que hayan escrito para enriquecer el
apunte de todos. |

| Propósito del video. Conocer, a través de ejemplos, la función de los números decimales y qué expresan, así como los usos de la multiplicación de decimales. |
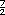 x
x 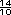 =
= 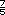 =
= 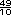 = 4.9
= 4.9
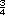 o 0.75
o 0.75